|
 |
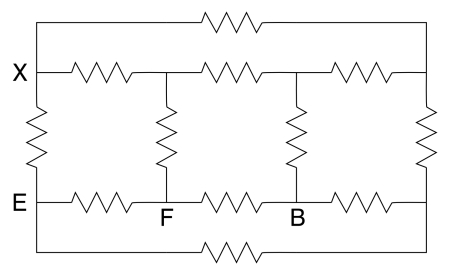
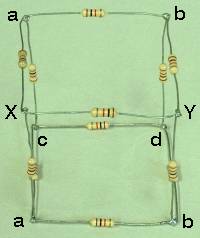
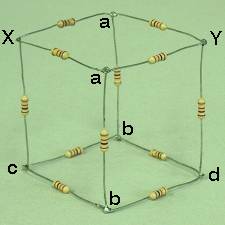
This is a popular puzzle, and it appears as problem 35 in chapter 32 of Physics (third edition, part 2) by David Halliday and Robert Resnick. The resistor cube in the photographs above is composed of 12 1,000-ohm resistors. The idea is to calculate the resistance between any two points on the cube, for which there are three possibilities. You can calculate the resistance across an edge of the cube, across a face diagonal or across a body diagonal. The figure below shows a schematic of the cube.
Points X and E are the ends of a cube edge, X and F give a face diagonal, and X to B gives a body diagonal. You could draw an arbitrary (DC) voltage source across X and E, X and F or X and B, and then using Kirchoff's rules (that the algebraic sum of the currents at any circuit junction must equal zero, and that the sum of the changes in potential encountered in making a complete loop equals zero), derive six equations in six unknowns for the currents in terms of the voltage and the various resistances, then solve the equations to find the total current and thus the overall resistance. Since all the resistors are identical, however, we can take advantage of the symmetry of the cube and solve the problem in a much simpler way.
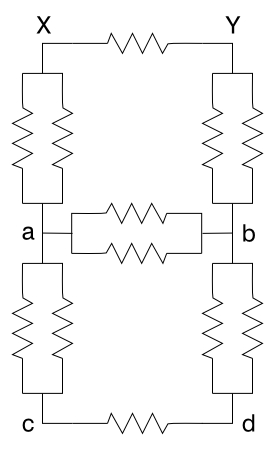
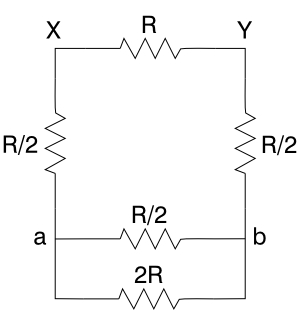
First, let us start with the resistance along a cube edge. In the photograph below, the cube is oriented to make the symmetrical arrangement easier to see. The currents going into and out of points X and Y must split equally along both resistors attached to each, and then combine equally through the bottom two pairs. So we see that the points marked ‘a’ must be at the same potential, and those marked ‘b’ must be at the same potential. If two points in a circuit are at the same potential, we may think of them as if they are connected by a wire. If we do this, we arrive at the schematic shown on the right.
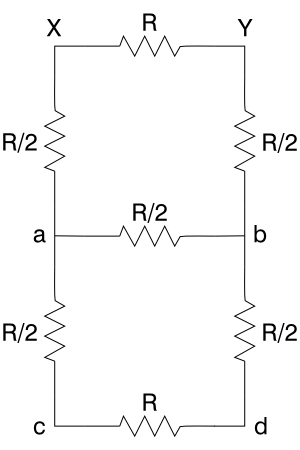
Since resistors add reciprocally in parallel (that is, 1/RTOT= 1/R1+1/R2+. . .+1/Rn), if we call the value of each resistor R, then each parallel pair equals R/2, and our schematic becomes:
which by adding the three bottom resistors in series (RTOT= R1 + R2 + . . . + Rn) we can further simplify to: The parallel combination of R/2 and 2R gives 1/RTOT= 2/R+1/(2R) = 5R/2R2, and RTOT= (2/5)R. Added in series with the two resistors of R/2, this gives a parallel combination between X and Y of R and (7/5)R. For the edge, then, 1/RTOT= 1/R + 5/(7R) = 12R/7R2. The total resistance across the edge is thus (7/12)R. With R = 1 kohm (or 1 k), this equals 583 ohms.
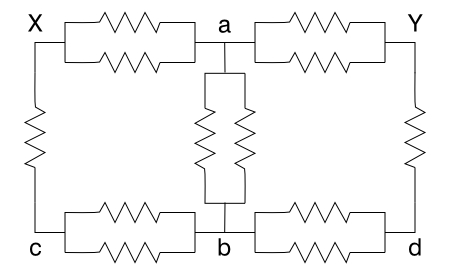
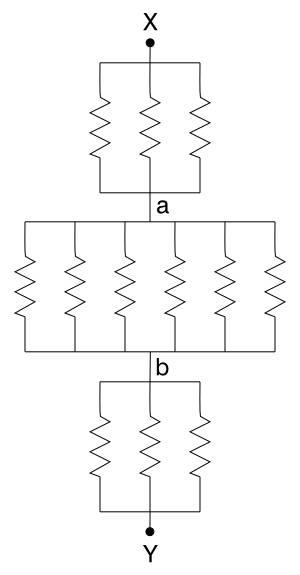
Next, we’ll do a face diagonal. As for the edge, the photograph below shows the cube in an orientation that helps make the symmetry clear. Again, if we imagine a potential placed across the cube at points X and Y, by symmetry we can see that points a are at the same potential, and so are points b, to give us the schematic shown on the right.
Again, all the parallel combinations add to give R/2, and we have:
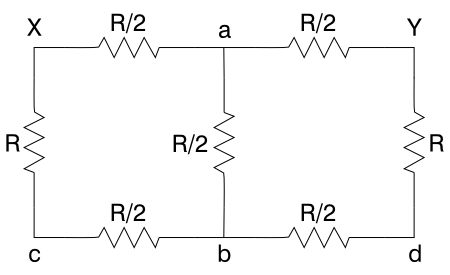
When we add the two pairs of series resistors (R + R/2 = 3R/2), we get:
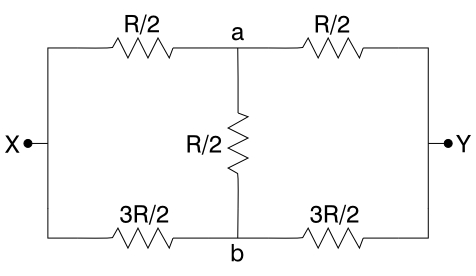
At first, this schematic looks a bit tricky, but we note that the resistances on either side of point a are equal, and so are those on either side of point b. Thus, both point a and point b are at a potential halfway between that at X and that at Y, and so are at the same potential. It therefore does not matter whether or not the resistor of R/2 that connects points a and b is there. If we consider it a dead short, we get the sum of twice the parallel combination of R/2 and 3R/2. This parallel combination is: 1/RTOT= 2/R + 2/(3R) = 8R/3R2; RTOT = (3/8)R. Two such combinations added in series give (3/4)R. If we treat the circuit as if the resistor between a and b is not there, we get the parallel combination of R and 3R: 1/RTOT= 1/R + 1/(3R) = 4R/3R2; RTOT= (3/4)R, which for R = 1 k equals 750 ohms.
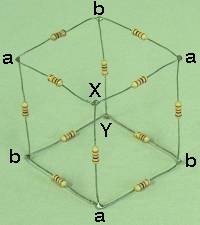
Last, we look at the body diagonal. Again, the photograph shows the cube in such an orientation as to make the symmetry clear. Since the points a are equidistant from points b and vice versa, the currents must split equally in the resistors going from X to a and from Y to b, and the currents in all the resistors connecting points a and points b must also be equal. Thus, points a are all at the same potential, and points b are also at the same potential. This gives us the schematic shown on the right.
This is merely the series sum of three parallel arrangements, or R/3 + R/6 + R/3, which equals (5/6)R. For R = 1 k, this equals 833 ohms.
You can measure the resistance across an edge, face diagonal or body diagonal by attaching the ohmmeter probes as shown in the top photo, and use the large display to show the results to the class. The values you measure will, of course, be close to the ones calculated above. (The tolerance on the values of the resistors in this cube is 5%.)