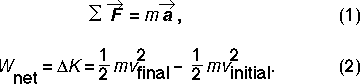Challenges in Teaching and Learning Introductory Physics

This article first appeared in a Festschrift for Professor William A. Little of Stanford University: From High Temperature Superconductivity to Microminiature Refrigeration, B. Cabrera, H. Gutfreund, and V. Kresin, eds. (Plenum, New York, 1996), pp. 313-322. ©1996 Plenum Press, New York.

INTRODUCTION

In a volume intended to celebrate Bill Little's many contributions to fundamental and applied research in physics, an article about teaching the most elementary aspects of physics may seem somewhat out of place. But a substantial part of Bill's well-deserved reputation is based on his excellence as a teacher, especially for the introductory courses for engineers and biological science majors. This article is offered in homage to his tradition of excellence in education.

During his distinguished career, Bill has served as a mentor to a great number of graduate teaching assistants. In large part, I owe what success I have had as a physics educator to what I learned from Bill during my own teaching assistant days at Stanford. My goal in this article is to attempt, however feebly, to carry on his tradition.

In particular, I will discuss some aspects of the introductory physics course that will be of interest (and perhaps surprising) to new college physics teachers and new teaching assistants. I hope that this article will also be of use to the "old hands" who, like me, discover something new about teaching every time they go into a classroom or talk with a student.

The challenges involved in teaching an introductory course in physics are legion, so my goal in this brief article is not to be comprehensive --- merely provocative! References 1 and 2 include a variety of other tips and suggestions for physics faculty and teaching assistants.

WHY INTRODUCTORY PHYSICS EDUCATION IS IMPORTANT

The relative importance of teaching in the physics enterprise has increased dramatically in recent years. As federal funding for research decreases, the golden era in which newly-minted physics Ph. D.s were guaranteed at least a postdoctoral research position is becoming an ever more distant memory. A larger fraction of the available academic positions emphasize teaching, especially at four-year and two-year colleges. Even at research universities, teaching is now playing a larger role in promotions and tenure decisions. In this brave new world, a physics graduate student who aspires to an academic career dare not neglect the teaching side of her or his graduate training.

While teaching physics at all postsecondary levels --- beginning undergraduate, advanced undergraduate, and graduate --- is important, the greatest importance attaches to the introductory courses taken by students in their first two years of college. For the budding physics major, these courses are the ones in which the student gets his or her first taste of the subject and decides whether or not to pursue the bachelor's degree in physics. The basic understanding achieved in these courses is the foundation for all subsequent study in physics.

The real importance of the introductory courses, however, lies in those students who are not physics majors. Indeed, the vast majority of students in introductory courses are likely to be engineers (in a calculus-based course), premedical students (in an algebra-based course), or humanities majors (in a "conceptual physics" course). These students constitute the educated electorate of the future, and their introductory physics courses are the only chance that we physicists have to plead our case with them.

The dominant public perception of physics is that it is tedious, abstract, and fundamentally irrelevant; the challenge in an introductory course is to convince the audience that physics is rewarding, fun, useful, and most of all a worthwhile endeavor. If we fail in this, and the public perception of physics does not change, there is little chance that future physics research will be funded at anything more than a token level. In this sense, introductory physics teaching is the foundation not only of a physics education, but of the physics enterprise as a whole. We neglect the teaching of these courses at our own grave peril.

WHY JOHNNY CAN'T ANALYZE CIRCUITS

College students begin most of their courses in a state of nearly perfect tabula rasa. Before they take their first course in world history, in economics, or in psychology, they know little or nothing about those subjects. The instructor can then help the students to implant fresh knowledge upon the palimpsests of their minds.

The situation in an introductory physics course is quite different. Although they would be shocked to hear you say it, students arrive in their first physics course with a set of physical theories that they have tested and refined over years of repeated experimentation. How can this be? The reason is that students have spent some eighteen years exploring mechanical phenomena by walking, running, throwing baseballs, catching footballs, and riding in accelerating vehicles. They have also some more limited experience with electrical phenomena, garnered from using electric circuits in the home, and about the behavior of light, lenses, and mirrors. Based on their observations, students have pieced together a set of "common sense" ideas about how the physical universe works.

Unfortunately, research carried out by physicists has shown these "common sense" ideas are in the main incompatible with correct physics. Worse still, these erroneous ideas are robust and difficult to dislodge from students' minds, in large measure because these ideas are not addressed by conventional physics instruction.

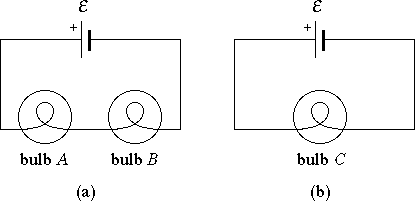
As an example, Fig. 1 illustrates some representative "common sense" ideas about electric circuits. In part (a) of the figure, a battery is connected to two identical light bulbs A and B in series. In part (b), the battery is connected to a single bulb C which is identical to bulbs A and B. McDermott and Shaffer [3] asked students in introductory physics courses to compare the brightnesses of bulbs A and B in circuit (a) and to compare these with the brightness of bulb C in circuit (b).

The results of this investigation were incredibly disappointing. The correct answer, that bulbs A and B in circuit (a) are equally bright and that bulb C in circuit (b) is brighter still, was given by only about 10% of the students in algebra-based courses and by only about 15% of the students in calculus-based courses.

The most remarkable result of McDermott's and Shaffer's study is that the types of student errors made on this question are unrelated to, and unaffected by, conventional instruction. One common student error is the belief that in circuit (a), bulb A will be brighter than bulb B because bulb A "'uses up' the current first." Another common error is that the brightness of each bulb will be the same in either circuit because the battery provides a constant current in all cases. Neither of these incorrect ideas are learned from an introductory course, but neither are they discredited in a standard introductory course. Indeed, McDermott and Shaffer found that student performance on this question was nearly independent of whether the question was posed before or after instruction on electric circuits. Similarly disquieting results have been found regarding "common sense" ideas in mechanics [4] [5] [6] and in optics [7].

Investigations of this sort show that it is not enough to merely teach students the right way to think about physics. Rather, the challenges to the instructor are to identify possible student misconceptions, to confront these misconceptions head-on, and to help students to unlearn these misconceptions at the same time that they are learning correct physics. Failure to do this will invariably leave students with their erroneous "common sense" ideas intact.

In order to rise to these challenges, an essential tool is an introductory physics textbook that addresses "common sense" ideas explicitly. Sadly, most contemporary textbooks are severely deficient in this respect. But some very recent textbooks make extensive use of research into student misconceptions [8] [9], and these should be given consideration by instructors who are serious about helping students overcome their "common sense" ideas about physics.

"I UNDERSTAND THE CONCEPTS, I JUST CAN'T DO THE PROBLEMS"

Every physics instructor has heard this complaint from students at one time or another. All too often, however, what the student really means is the converse:

"I can do (some of) the problems, I just don't understand the concepts."

Students can usually handle problems that are akin to the worked examples in their textbook, especially if there are "special equations" that they can use. Problems that require using fundamental concepts, along the lines of how we might expect a physicist to think, are another matter altogether.

The proof of this statement is the difference between student performance on "standard" physics problems that require computation and calculation and their performance on purely conceptual, qualitative problems. As an example, McDermott and Shaffer [3] found that even students who performed well on standard numerical problems in circuit analysis, and even students with near-perfect scores on such problems, performed poorly on the conceptual question depicted in Fig. 1.

Part of the difficulty that students have with conceptual questions stems from the kind of problems that students are most often assigned. Instructors commonly assign homework and exam problems that involve computation or calculation, in the belief that these are "real" physics problems. A corollary to this belief is the assumption that a student's ability to successfully solve such problems is evidence of complete understanding. Alas, research shows that such is not the case. One example is an investigation of student understanding of the Newtonian concept of force carried out by Hestenes, Wells, and Swackhamer. [6] By comparing student performance on a set of conceptual questions posed both before and after a first course on mechanics, they found that conventional instruction (including the assignment of conventional homework problems) produces only marginal gains in conceptual understanding.

If we truly want students to learn about the ideas of physics, we must require them to use these ideas in their homework and then hold them accountable for these ideas in examinations. Most introductory textbooks include a wealth of conceptual questions, and questions of this sort these should be assigned regularly. My own students regularly comment that they find conceptual questions to be much more difficult than the "ordinary" problems; such comments convince me that conceptual questions are very useful tools for teaching and learning physics.

WHAT DOES THAT EQUATION MEAN?

A related issue is the question of how students deal with formal, mathematical expressions of physical concepts. Two examples are Newton's second law and the work-energy theorem:

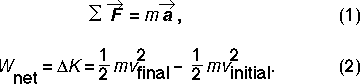
It is very common for students to interpret Eq. (1) to mean that the product of a body's mass and its acceleration is itself a force. In other words, they fail to realize that a mathematical equality between two quantities does not imply that the two quantities are conceptually distinct. As a result, they do not appreciate that acceleration is the consequence of the presence of a net force. Thus students frequently make reference to such chimera as "the force due to acceleration" or "the force due to momentum."

A similar confusion arises concerning the work-energy theorem, Eq. (2). When students are asked to explain what kinetic energy means, the most common response is that it is "one-half the mass times the speed squared." By fixating on the mathematical definition, they fail to grasp the essence of the work-energy theorem: that the kinetic energy of a particle is equal to the total work that was done to accelerate it from rest to its present speed, and equal to the total work that the particle can do in the process of being brought to rest.

This tendency to focus on a mathematical definition rather than physical meaning was shown convincingly by Lawson and McDermott. [10] They presented students with a simple question concerning the work-energy theorem. As depicted in Fig. 2, an object of mass m and another object of mass 2m are initially at rest on a frictionless horizontal surface. The same constant force of magnitude F is then applied to each object. The question to be answered is "Which object crosses the finish line with greater kinetic energy?"

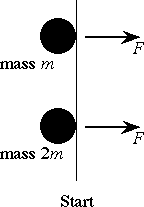Figure 2. A top view of a "race" between two objects on a frictionless horizontal surface. The two objects are of different mass but are subjected to the same net force. When asked which object crosses the finish line with greater kinetic energy, only a few students were able to give the correct answer.

Using the work-energy theorem, and keeping in mind the physical meaning of kinetic energy, it can easily be seen that each object has the same kinetic energy upon reaching the finish line. Yet in interviews with 28 students taken from two classes at the University of Washington, an honors section of calculus-based physics and a regular section of algebra-based physics, Lawson and McDermott found that only a few honors students were able to supply the correct answer and the correct reasoning without coaching. While most of the remaining honors students were able to eventually achieve success with guidance from the interviewer, almost none of the students from the algebra-based course were able to do so. No less disappointing results were obtained with a written version of the question presented to a regular section of calculus-based physics. I have had similar experiences with my own students: Their performance on conventional homework-type problems shows that they can compute quantities such as work and kinetic energy, but their performance on conceptual questions shows that they have much more difficulty explaining or interpreting their results.

This example shows again that emphasis on numerical problem-solving can obscure major conceptual deficiencies in students. It underscores the importance of requiring students to apply the fundamental concepts of physics in a variety of different situations, as well as requiring them to explain the logic that they use in solving physics problems of all kinds.

RETHINKING THE LECTURE AND DISCUSSION SECTION

A point that I have stated repeatedly in this article is that conventional physics instruction tends to be ineffective in helping students to develop a real understanding of physics. How, then, should the nature of physics instruction be changed? A number of different approaches have been suggested and explored; I will summarize the approaches that I believe to be the most promising.

The Misuses of the Lecture

The lecture is one of the most ancient of teaching methods. In the teaching of physics, it is typically used to demonstrate physical phenomena, to present derivations; and to show examples of how to solve problems. The first of these uses of the lecture is an important one, and is often neglected by instructors who feel compelled to "cover more material" or who regard the demonstrations as a distraction. My own experience is that good lecture demonstrations are absolutely indispensable as tools for helping students to relate physical concepts to the real world. Good lecture demonstrations also have the strength of being memorable. I have had students come to me a decade after taking one of my classes and tell me how they still remember a certain demonstration and the physics that they learned from it. (By contrast, I have yet to have a former student tell me how vividly they remember my derivation of the thin-lens formula.) The title "Lecture Demonstrator" is still in use at certain British universities to denote a science lecturer; the title alone speaks volumes about the importance of lecture demonstrations.

By contrast, the use of lecture time to present derivations is typically ineffective. A derivation presented on the blackboard is less useful to the student than the same derivation presented in the textbook, where it can be traced through repeatedly at the student's leisure. My suspicion is that instructors tend to present derivations in lecture because they doubt that their students read the book. While this is indeed a valid concern, it would seem that using the lecture to reiterate the contents of the book is ultimately counterproductive; it merely helps to ensure that the students won't read the book.

Far and away, however, the least effective use of lecture time is for presenting the solutions to physics problems. The essential difficulty here is that physics problem-solving is a skill that has to be learned by repeated practice. In learning a skill, it can be useful to first watch an expert exercise that skill, but that is by no means the most important part of the learning process. If it were, the millions who watch professional sports would themselves naturally develop into top-notch players; avid movie-goers would inexorably turn into accomplished actors (who really want to direct); and the poor souls who watch televised court proceedings would slowly but surely mutate into highly paid defense attorneys. Of course, none of these evolutions really take place. In the same way, students who watch their instructor (an expert problem-solver) work out a solution on the board may be impressed by the instructor's prowess, but they will augment their own problem-solving skills only marginally. The disappointing problem-solving performance of students who have had such conventional instruction, referred to earlier, is testimony to this.

A Lecture Model with "Active Learning"

Numerous instructors, myself included, have found that lectures become more useful when students are forced to become active participants in the lecture. [11] In my own classes, I speak briefly about each new topic (proceeding under the assumption that students have read the required material from the textbook before class), and do a lecture demonstration or two as appropriate. I then give the students an exercise to work out. They then spend several minutes working out this exercise, which is chosen to be specific to the topic at hand: it may involve tasks such as drawing free-body diagrams, writing down (but not necessarily solving) the key equations for a group of related but distinct situations, or making graphs of different types of motion. While this is going on, I roam around the classroom inspecting the students' work. I then instruct the students to confer with their neighbor to compare their responses and to resolve any discrepancies. Remarkably, this works very well even in a large lecture hall; the sound level from the discussions among 300 students can be quite impressive! Finally, I discuss with the students the correct way to tackle the exercise, being careful to point out common errors to the students. I typically do two or three sequences of instructor description --- student work --- instructor discussion during a typical lecture.

This technique has several merits. First, the students have something constructive to do during the lecture; it is a sure-fire cure for the torpor that grips students midway through a conventional lecture. Second, students are forced to discuss physics with their peers and to defend their ideas. Third, students get immediate feedback as to whether or not they understand a concept that has been presented in class, and any points of confusion can be corrected at an early stage in the students' apprehension of the concept. Last, but by no means least, the instructor can learn a great deal about her or his students' understanding of the material. This last point was brought home to me vividly during a lecture when I asked students to draw the free-body diagram for a car rounding a banked curve; many of the diagrams I saw while walking around the lecture hall included a number of creative and wholly imaginary forces that I had never dreamed existed!

When conducting the lecture in this way, it is best if the students have a printed sheet with the exercise on it. These can be time-consuming to develop and to prepare in printed form, however. I have relied heavily on Alan Van Heuvelen's ALPS Kit (an acronym for Active Learning Problem Sheets), and Randy Knight's Student Workbook for Physics: A Contemporary Perspective, which are workbooks containing several hundred exercises and activities expressly designed for student use during lecture. [12] Students purchase these inexpensive workbooks at the campus bookstore, and are required to bring them to lecture; happily, I find that almost all of them do so religiously.

Some will no doubt complain that this technique of "active learning" forces the lecturer to cover less material. It is indeed true that the lecturer talks about less material with this approach; the challenge to the lecturer is to choose between the material that is worthy of discussion during the lecture and the easier material that the students can learn adequately on their own from the textbook. Thus this technique does not require that any material be deleted from the course syllabus.

Employing "active learning" in the lecture keeps students engaged in the lecture. More importantly, it yields substantially better student performance on exams than does conventional instruction. [11] [12]

Discussion Sections,Teaching Problem-Solving, and "Cooperative Learning"

Most introductory physics courses have both a lecture component and a discussion section (or "recitation section") component. The discussion section, typically led by a teaching assistant (TA), is intended principally to be a forum in which students gain insight into problem-solving technique by observing the discussion leader, by practicing solving problems, and by discussions with other students.

Unfortunately, physics discussion sections very often fail to live up to this intent. Too many students come to discussion sections with the intent that they will get their weekly homework "done for them" by the TA. As a result, despite the earnest efforts of hard-working and talented TAs, it is difficult to cajole students into actually doing problem-solving work in a discussion section. Furthermore, it is next to impossible to initiate and sustain any real student discussion within the unstructured format of a typical discussion section. The upshot is that few students are able to move beyond the "formulaic" approach to problem-solving, which consists of hunting through the textbook for a likely-looking equation or set of equations into which they can plug the values stated in the problem. This sad state of affairs is especially frustrating for TAs who, after working diligently with a group of students for an entire term, must grade those students' disappointing work on exams.

A very promising effort to rectify these shortcomings of the discussion section has been described by Heller, Keith, Anderson, and Hollabaugh. [13] [14] They reorganized the discussion sections in two rather different physics courses, the first quarter of a large algebra-based introductory course at the University of Minnesota and a sophomore modern physics course with a dozen students at Normandale Community College. In both courses, students were taught a general problem-solving strategy based on the methods used by expert problem-solvers, and were required to write up their problem solutions in a way that explicitly reflects the use of that strategy. (In addition to shaping the students' approach to problem-solving, this technique helps to clarify for the grader what conceptual ideas the students are using.) To discourage "formulaic" problem-solving, students were assigned so-called "context-rich" problems. Such problems do not always explicitly identify the unknown variable, may include extraneous information, and may require reasonable assumptions (e. g., the acceleration is constant) or estimation (e. g., the mass of a typical cat). In other words, they are less like standard textbook problems and more like the problems encountered by real scientists and engineers. The folowing is an example of such a "context-rich" problem, taken from Ref. 14:

Such "context-rich" problems are of the kind that we would like our students to be able to solve, but which are usually thought too difficult and challenging for students to solve on their own. Remarkably, students in both of the test groups described in Refs. 13 and 14 were able to solve such problems when each discussion section was organized into cooperative groups of three students. The students in each group were required to work together to produce a group solution to the assigned problem, using the problem-solving strategy that they had been taught. All students in the group received the same grade for their group assignment. The students in each group were assigned the roles of Manager (who keeps the group on task and manages the sequence of steps), Skeptic (who helps the group to avoid overly quick agreement and asks questions like "Are there other possibilities?"), and Checker/Recorder (who checks for consensus among the group and who writes up and hands in the group solution). These roles were rotated among the students each week. The use of such definite roles, and the challenging nature of the assigned "context-rich" problems, kept the students from simply working independently.

To reinforce the use of the problem-solving strategy and of the skills used in the cooperative groups, each course exam included a "context-rich" problem that had to be solved by the students in their cooperative group during the discussion section. (More conventional individual exams were given during lecture.)

Heller et al. found that over two quarters of using these methods, the problem-solving technique of students of all ability levels improved. [13] It may not be surprising that this proved to be the case for students in the lowest third and middle third of the class. The structured problem-solving strategy and the requirement to discuss ideas with other students seems well-suited to helping students whose understanding of problem-solving was initially only fair or poor. What is remarkable is that participation in cooperative groups also helped the best students in the class to improve their problem-solving skills, and that these students improved at about the same rate as the students in the lowest and middle thirds. For example, the percentage of students in the lowest third of the class whose individual solutions followed a logical mathematical progression improved from 20% to 50% over two quarters; this percentage for students in the upper third improved from 60% to 90%. Furthermore, this improvement of all students was found in both group problem-solving and individual problem-solving.

The use of cooperative groups and "context-rich" problems can have a very beneficial effect on student problem-solving skills. We have just begun to implement these innovations in the introductory calculus-based physics course at UC Santa Barbara, and the preliminary results look encouraging. This method is not a panacea, however; Heller at al. found that their innovations did not have much beneficial effect on students' understanding of the conceptual aspects of physics. [13] This suggests that these aspects are best addressed in the lecture using the "active learning" technique described previously.

CONCLUSION

Teaching and learning introductory physics are both challenging tasks. While traditional methods have led to frequently disappointing results, I have tried to show that there is hope. As instructors, we should heed the lessons about our students' thought processes learned from research into "common sense" ideas about physics and into students' difficulty with formal mathematical reasoning. We must see to it that students truly learn how to use the concepts of physics, in order that they may learn how to think like a scientist or engineer. And we should be willing to consider new forms and new approaches for the time-honored lecture and discussion section. Whatever gains we can make in improving student understanding and appreciation of physics cannot help but improve the public perception of physics as a useful, interesting, and above all comprehensible human activity.

ACKNOWLEDGEMENTS

I thank my many teachers at Stanford for helping to cultivate my interest in the field of physics education. In particular, I thank Alan Schwettman, Dirk Walecka, and especially Bill Little for his service as a role model to generations of Stanford graduate student TAs.

REFERENCES

1. A. B. Arons, Teaching Physics, Wiley, New York (1997). [First appearance in article]

2. M. J. Bozack, Tips for TA's: The role of the physics teaching assistant, Phys. Teach. 21, 21 (1983). [First appearance in article]

3. L. C. McDermott and P. S. Shaffer, Research as a guide for curriculum development: an example from introductory electricity, Part I: Investigation of student understanding, Am. J. Phys. 60, 994 (1992). [First appearance in article]

4. I. Halloun and D. Hestenes, The initial knowledge state of college physics students, Am. J. Phys. 53, 1043 (1985). [First appearance in article]

5. I. Halloun and D. Hestenes, Common-sense concepts about motion, Am. J. Phys. 53, 1056 (1985). [First appearance in article]

6. D. Hestenes, M. Wells, and G. Swackhamer, Force concept inventory, Phys. Teach. 30, 141 (1992). [First appearance in article]

7. F. M. Goldberg and L. C. McDermott, An investigation of student understanding of the real image formed by a converging lens or concave mirror, Am. J. Phys. 55, 503 (1987). [First appearance in article]

8. L. C. McDermott, Physics by Inquiry, Wiley, New York (1996). [First appearance in article]

9. H. D. Young and R. A. Freedman, University Physics, 9th edition, Addison-Wesley, Reading, MA (1996). [First appearance in article]

10. R. A. Lawson and L. C. McDermott, Student understanding of the work-energy and impulse-momentum theorems, Am. J. Phys. 55, 811 (1987). [First appearance in article]

11. A. Van Heuvelen, Learning to think like a physicist: A review of research-based instructional strategies, Am. J. Phys. 59, 891 (1991). [First appearance in article]

12. A. Van Heuvelen, Overview, Case Study Physics, Am. J. Phys. 59, 898 (1991); R. D. Knight, Student Workbook for Physics: A Contemporary Perspective (Addison-Wesley, Reading, MA, 1998). For information on how to obtain the ALPS Kit, contact Professor Alan Van Heuvelen, Department of Physics, Ohio State University, Columbus OH 43210-1106. [First appearance in article]

13. P. Heller, R. Keith, and S. Anderson, Teaching problem solving through cooperative grouping, Part 1: Group versus individual problem solving, Am. J. Phys. 60, 627 (1992). [First appearance in article]

14. P. Heller and M. Hollabaugh, Teaching problem solving through cooperative grouping, Part 2: Designing problems and structuring groups, Am. J. Phys. 60, 637 (1992).  [First appearance in article]

Go to beginning of article

Roger Freedman's main page