 |
 |
|
|
|
|
In this geometry a shear stress s is applied to the top and bottom of the material and a confining pressure p keeps the material from expanding. If s is large enough, the granular material will begin to move and eventually reach a steady state. This steady state is characterized by an average velocity <v(y)>, which depends on the vertical position y, and an average squared velocity <v2> which does not depend on position. The strain rate is defined as g = d<v(y)>/dt. These average velocities must be somehow related to the stresses s and p.
In order to derive a constitutive equation we rely on the Shear Transformation Zone (STZ) theory of amorphous solids that was first proposed at UCSB by Falk and Langer. STZ theory introduces variables that describe the internal, history dependent structure or state of a solid. These variables describe the state of the solid by specifying the number of regions in a dense material that are able to move non-affinely in order to flow. The shear rate can then be written in terms of the state variables. STZ theory is an example of a rate and state law. Combining STZ theory with a fundamental invariance in Newton's equations yields a relation between s, p, <v(y)>, and <v2>.
To test this relation we conduct computer simulations of sheared granular materials. Figure 2 is a movie of one such simulation. With these simulations we can measure s, p, <v(y)>, and <v2> independently. After many such simulations we obtain the data points shown in Figure 3. The bottom curve is for a granular material with no friction between particles and the upper curve has some amount of friction between particles. The line drawn through the data points is the prediction from STZ theory. As you can see, the agreement is very good, and we were the first group to accurately predict this flowing constitutive relations for dense granular materials.

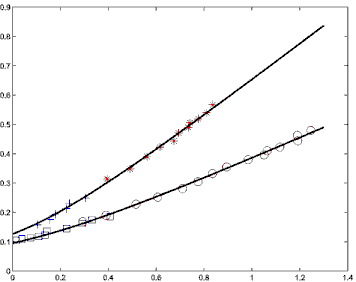
Figure 2 : A sample simulation
Figure 3: Data from simulations and fit from STZ
theory for s/p vs g/sqrt(<v2>)
We have learned a great deal applying STZ theory to granular materials,
but there are still many open questions:
(1) The constitutive relation in figure 3 only applies to steady
state flow. In the transient regime, where all of the variables have
non-zero time derivatives, STZ theory makes predictions on their time dependence.
These predictions must be understood and tested.
(2) STZ theory not only gives information about the flowing state
of a granular material, but also makes predictions about how a granular
material jams (transforms from liquid-like to solid-like behavior).
It is very important to understand and test these predictions as well.
(3) Many properties of granular materials depend on the distribution
of grain radii. Figure 3 was obtained with one distribution and it
would be interesting to know how the parameters in the STZ theory depend
on the distribution of grain radii.
(4) More conceptually, STZ theory is based on the fact that there
are regions in a granular material that are able to transform non-affinely.
One interesting line of research is whether these regions are related to
the force
statistics and/or contact statistics of the granular material.
(5) The study of sheared granular materials is closely related
to the study of friction in earthquake
faults . This relation should be explored further.
We hope to undertake these projects soon.
Papers on STZ theory and its application to Granular Materials:
STZ
Theory
Applying
STZ Theory to Granular Materials
Questions? Email Gregg Lois.