In order to calculate most any large scale parameter of a granular material (such as a stress), it is necessary to know the set of contacting particles and forces.   Because the large scale parameters are calculated from the small scale properties of individual grains, a general theory of granular materials must be able to predict these small scale properties.  While it is unlikely that any useful theory would be able to derive the exact small scale properties, a statistical determination would be very useful.

We have been working on creating simple theories that predict statistical measures.  The most interesting are: P(F), the probability density functional (PDF) to have a contact force of magnitude F;  <F(t)>, the PDF to have a contact force of magnitude F for a contact oriented with an angle(s) t;  and C(t), the PDF to have a contact oriented with angle(s) t.

The measure most studied in the physics literature is P(F).  For both flowing and jammed granular materials, P(F) is exponential at large forces.  At small forces the form of P(F) depends on the state of the granular material (see figure 1).  Most theoretical work has been concentrated on predicting P(F) for static, jammed granular assemblies.  Many of these theories use concepts from network theory or information theory.  We have been most interested in predicting P(F) for flowing configurations, and the work is ongoing.

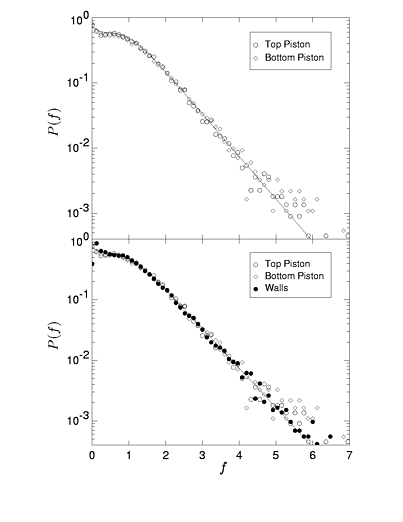
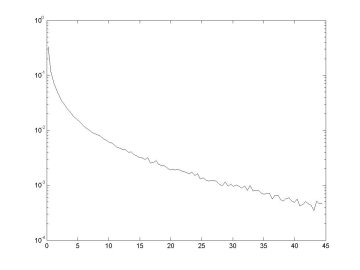
        Figure 1:
        Left:  Experimental P(F) for a jammed granular material from the granular physics group at Chicago.  This plot exhibits a peak at the average force.
        Right:  P(F) for a flowing granular material from our simulations at UCSB.  The peak disappears.

The other two statistical measures are shown for a flowing granular material in figure 2.  The functional form is very similar for jammed granular materials.  The portion of these functions we have concentrated on predicting are the second fourier components.  This is because knowledge of the second fourier components of these measures is enough to determine the ratio of shear stress to pressure s/p (see constitutive relations for definitions of s and p) .   This work is also ongoing.

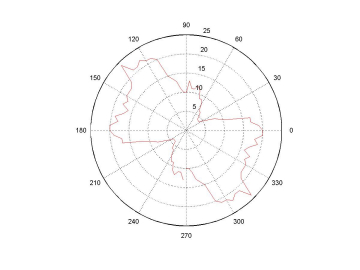
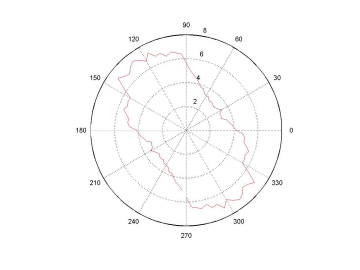
        Figure 2:
        Left:  Number of contacts as a function of angle.  Right:  Average contact force as a function of angle
 

The interplay of the contact geometry and force distributions produces force chains which are  the paths of force propagation in a granular material.  We show pictures of force chains for jammed and flowing granular materials in figure 3.  These chains are heterogeneously distributed through the material and one line of research we are interested in is whether we can create a theory that predicts the locations of force chains and whether the regions with a high density of force chains are related to the regions that contain a high density of STZ's.  In a jammed material these chains tend to percolate throughout the entire enclosure and for flowing materials they tend not to.   This observation has led many to link the size of force chains with the onset of jamming.  This is another line of research that we are interested in.

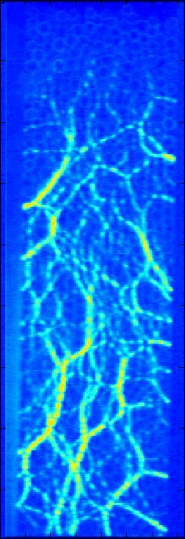
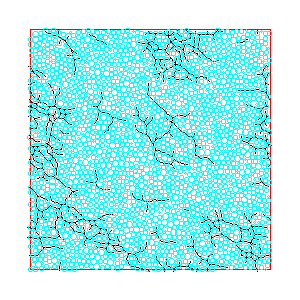
        Figure 3:
        Left-  Force chains for a jammed granular material from an experiment by the Behringer group at Duke.  The size of the line represents the
        magnitude of contact force between grains.
        Right-  Force chains for a flowing granular material from our simulations at UCSB.  A line is drawn between grains if there is a force (larger
        than some minimum value).
 

Questions?  Email Gregg Lois.