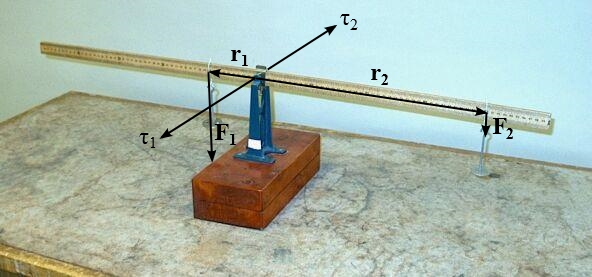
The meter stick in the photograph above is mounted on a knife-edge pivot placed at its center. Each mass hanger, with whatever masses are on it, exerts a torque about the pivot, which is τ = r × F, where r is the displacement vector from the pivot to the point from where the mass hanger is suspended, and F is the applied force, which is the weight of the hanger and masses, mg. Thus, by the right-hand rule, a torque exerted by a hanger suspended from the right side of the meter stick points inward (towards the back of the table in the photograph) from the pivot point, and one applied by a hanger suspended on the left side of the stick points outward from the pivot point. The magnitude of this torque is rmg sin θ, where θ is the angle between r and F. For the mass hangers, when the meter stick is horizontal, θ equals 90 degrees, sin θ equals 1, and τ = rmg. Torque, especially in this context, is often called the moment of force, and r is the moment arm. If the meter stick were not horizontal, then the moment arm for each mass hanger would be r sin θ, the perpendicular distance from the pivot to the point from which the mass hanger is suspended.

As noted above, each mass hanger exerts a torque that is opposite to that produced by the other. For the meter stick to balance, the moments must equal. That is, r₁m₁g = r₂m₂g, or r₁m₁ = r₂m₂. So for the meter stick in the photograph, since the moment arm of the mass hanger on the right (~0.4 m) is four times that of the one on the left (~0.1 m), the total mass on the left must be four times that on the right for the meter stick to balance as shown.

The meter stick as set up in this demonstration represents a class one lever. This is a lever for which the “load” and the “effort” are on opposite sides of the fulcrum. If the load is closer to the fulcrum than the effort, the lever is said to afford a mechanical advantage of the ratio of the moment arms, r_effort/r_load. For the meter stick in the photograph, if we consider the weight on the left to be the load, and take the weight on the right as the effort, the ratio of their moment arms is 40 cm/10 cm, which gives a mechanical advantage of 4:1, so, as noted above, the effort must be 1/4 the load to balance.

What does this have to do with work and energy?

If we wish to lift a load, then we need to apply slightly more than the load divided by the mechanical advantage. In the example in the photograph, this means making the effort slightly more than 1/4 of the load. If we did this, then the arm would pivot in a clockwise direction, with the load mass rising and the effort mass falling. The distance through which the effort mass falls is greater than that through which the load mass rises, in this case by a factor of four. To raise the load mass 1 cm, for example, the effort mass must fall by 4 cm. The work done in lifting the load is mg(0.01 m). The work done by the effort mass (or you, if you push on the meter stick yourself) is (m/4)g(0.04 m), which is the same as mg(0.01 m). Thus, the effort you exert to lift the load is a quarter of what you would need to lift it without the lever, but the work you do to lift it a given distance is the same as it would be without the lever.

References:

1) Resnick, Robert and Halliday, David. Physics, Part One, Third Edition (New York: John Wiley and Sons, 1977), pp. 231-233.