SUPERSTRINGS! String Basics

We are used to thinking of fundamental particles (like electrons) as point-like 0-dimensional objects. A generalization of this is fundamental strings which are 1-dimensional objects. They have no thickness but do have a length, typically 10^(-33) cm [that's a decimal point followed by 32 zeros and a 1]. This is very small compared to the length scales that we can reasonably measure, so these strings are so small that they practically look like point particles. However their stringy nature has important implications as we will see.

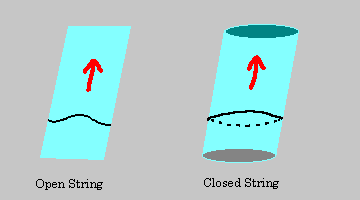
Strings can be open or closed. As they move through spacetime they sweep out an imaginary surface called a worldsheet.

world sheets

These strings have certain vibrational modes which can be characterized by various quantum numbers such as mass, spin, etc. The basic idea is that each mode carries a set of quantum numbers that correspond to a distinct type of fundamental particle. This is the ultimate unification: all the fundamental particles we know can be described by one object, a string! [A very loose analogy can be made with say, a violin string. The vibrational modes are like the harmonics or notes of the violin string, and each type of particle corresponds to one of these notes.]

As an example let's consider a closed string mode which looks like:

graviton

This mode is characteristic of a spin-2 massless graviton (the particle that mediates the force of gravity). This is one of the most attractive features of string theory. It naturally and inevitably includes gravity as one of the fundamental interactions.

Strings interact by splitting and joining. For example the anihilation of two closed strings into a single closed string occurs with a interaction that looks like:

interactions

Notice that the worldsheet of the interaction is a smooth surface. This essentially accounts for another nice property of string theory. It is not plagued by infinities in the way that point particle quantum field theories are. The analogous Feynman diagram in a point particle field theory is:

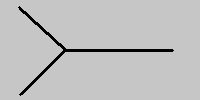
Feynman diagram

Notice that the interaction point occurs at a topological singularity in the diagram.

If we glue two of the basic closed string interactions together, we get a process by which two closed strings interact by joining into an intermediate closed string which splits apart into two closed strings again:
Animation of closed string scattering
This is the leading contribution to this process and is called a tree level interaction. To compute quantum mechanical amplitudes using perturbation theory we add contributions from higher order quantum processes. Perturbation theory provides good answers as long as the contributions get smaller and smaller as we go to higher and higher orders. Then we only need to compute the first few diagrams to get accurate results. In string theory, higher order diagrams correspond to the number of holes (or handles) in the world sheet.
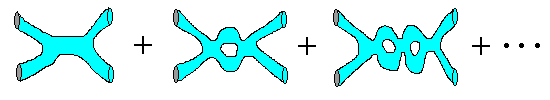
Loop diagrams
The nice thing about this is that at each order in perturbation theory there is only one diagram. [In point particle field theories the number of diagrams grows exponentially at higher orders.] The bad news is that extracting answers from diagrams with more than about 2 handles is very difficult due to the complexity of the mathematics involved in dealing with these surfaces. Perturbation theory is a very useful tool for studying the physics at weak coupling, and most of our current understanding of particle physics and string theory is based on it. However it is far from complete. The answers to many of the deepest questions will only be found once we have a complete non-perturbative description of the theory.