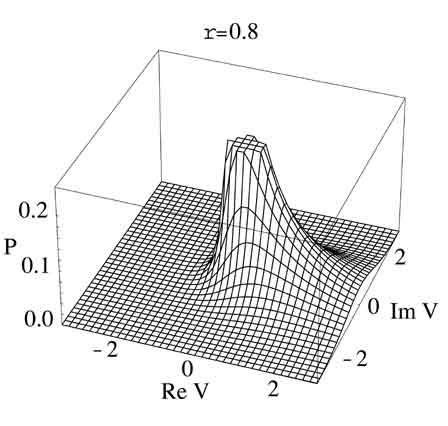
Distribution of the product of complex numbers drawn from covariant Gaussian distributions, with covariance 0.8.

Noiselike Signals: Nearly all signals from astrophysical sources are noise. More precisely, one sense of polarization of the electric field from an astrophysical source at any instant is drawn from a complex Gaussian distribution. (The real and imaginary parts represent the instantaneous phase of the signal.) All the interesting parameters of the source -- spectrum, size, polarization, and so on -- can be expressed as the variance of that Gaussian distribution, or its mean square; and as the covariances among the noises measured at different times, places, polarizations, and so on. These variances and covariances completely characterize the signal.

Correlated Noise: In radio astronomy, the statistics of the Gaussian distribution are often measured by correlation. Specialized correlators multiply electric fields together and average their product, to determine their covariance. For reasons similar to the success of digital cell phones, music, and video, radio-astronomical signals are usually digitized: digitized signals can be amplified and transmitted much more easily. Of course, the process of digitization reduces the amount of information in the signal. A fundamental understanding of the consequences of digitization and multiplication on Gaussian noise is important to understanding the statistics of astrophysical measurements.

• The product of correlated elements drawn from Gaussian distributions and multiplied together has an interesting probability distribution, as shown above.
  Gwinn 2001, ApJ, 554, 1197
  
  
• Description of continuous signals as a set of discrete levels (a part of the digitization process known as quantization) destroys some of the information in the signals. Quantization changes both the deterministic and random parts of the correlation (that is, the signal and the noise) when the signals are correlated, in a way that can be calculated mathematically. Perhaps surprisingly, correlation of quantized signals can yield higher signal-to-noise ratio than would correlation of the original, continuous signals!
  "Correlation Statistics of Quantized Noise", C.R. Gwinn, PASP, 116, 84 (2004)
  
  
• The spectrum of a source is the Fourier transform of the autocorrelation function. Radiotelescopes often apply this fact to measure spectra, from autocorrelation of a signal using an autocorrelator; or from cross-correlation of two spectra, to find the cross-power spectrum. Quantization affects the signal and noise of the result, for both cross- and autocorrelation.
  "Correlation Statistics of Spectrally-Varying Quantized Noise", C.R. Gwinn, PASP, 118, 461 (2006)
  

• Propagation through a scattering, dispersing or absorbing medium is well approximated by a convolution.  Propagation of a signal from a noiselike source with intermittent emission, such as a pulsar, leaves the average spectrum, average correlation function, and distribution of noise in the spectrum unchanged; however, intermittency changes the distribution of noise in the correlation function, and introduces correlations among noise in different channels of the spectrum.
  "Noise and Signal for Spectra of Intermittent Noiselike Emission", C.R. Gwinn and M.D. Johnson, ApJ in press (2011).
• Poster for Visit Day, 4 April 2011.
  

• Inventory of noise for the pulsar B0834+06, as observed with VLBI and single-dish spectrometers, matches theoretical expectation, as long as effects of intermittency of the pulsar on short, intermediate, and long timescales are included in the analysis.
  "Effects of Intermittent Emission: Noise Inventory for Scintillating Pulsar B0834+06", C.R. Gwinn, M.D. Johnson, T.V. Smirnova, and D.R. Stinebring, ApJ in press (2011).
  
• WAPP Data
• VLBA Data