Complex Systems

A vision shared by most researchers in complex systems is that certain intrinsic, perhaps even universal features capture fundamental aspects of complexity in a manner which transcends specific domains. It is in identifying these features that differences arise. In disciplines such as biology, engineering, sociology, economics, and ecology, individual complex systems are necessarily the objects of study, but there often seems to be little common ground between their models, abstractions, and methods. Highly Optimized Tolerance (HOT) is a recent attempt to develop a general framework for studying complexity, which was introduced by Carlson and Doyle. The HOT view is motivated by examples from biology and engineering, and builds theoretically on the abstractions from control, communications, and computing. A central component of our research program involves extending this theoretical framework.

HOT emphasizes 1) highly structured, non-generic, self-dissimilar internal configurations and 2) robust, yet fragile external behavior. In HOT these features are inherent, important features of complexity, not accidents of evolution or artifices of engineering design, but rather inevitably intertwined and mutually reinforcing. HOT provides an appealing base for the development of a general framework for understanding a broad spectrum of complex systems. Questions related to robustness, diversity, predictability, verifiability, and evolvability arise in a wide range of disciplines, and demand sharper definitions, and new tools for analysis. The success of HOT came from first studying tractable, broadly accessible models, from which we extract qualitative insights and quantitative analysis which can be applied to specific problems.

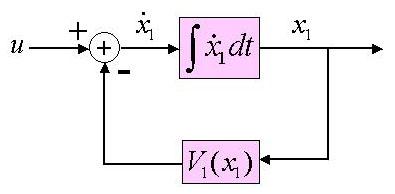
HOT blends the perspectives of engineering control theory with the simple models of statistical physics. While physics focuses primarily on universal properties of generic ensembles of isolated systems, control theory studies open systems in terms of their input vs. output characteristics, and has the flexibility to describe systems which are highly structured and extremely non-generic in a systematic way. Currently, we are moving further in developing links between the mathematics of control theory and fundamental problems in statistical physics by using model reduction on finite time horizons to derive rigorous links between statistical physics, thermodynamics, and measurement. Model Reduction and other mathematical methods have been developed with precision in control theory, but their consequences outside of that discipline are largely unexplored. Many of these methods when properly generalized will become the building blocks for quantitative analysis of complex systems across a broad range of disciplines.

Even within statistical physics and quantum theory there are situations where mathematics from control theory can lead to a more rigorous theoretical foundation. This is particularly true where the coupling between a system and the environment must be explicitly taken into account, as in the case of dissipation and quantum measurement. The opportunities for developing a more quantitative theoretical foundation which extends to other disciplines is extremely promising. In areas such as biology, ecology, sociology, and finance, systems are necessarily open, highly structured, and involve a great deal of feedback, so they are clear candidates for methodologies from controls.