Physics CS 33
|
Set # 2
|
Spring 2006
|
| Due date |
Wed. April 19th
|
Read HR&K:
|
Chapter 16
|
| Read
K&K: |
None
|
|
| HR&K
Problems: |
Chapter 15 Problem 19
Chapter 16 Problems 3, 4, 8, 11,
14, 15
|
K&K
Problems:
|
None
|
|
| 1. |
A raindrop has a
mass of one gram. Assuming it is perfectly spherical, find the
pressure of the water inside the raindrop. Use 1000 kg/m3
for the density of water and ignore the variation of pressure within
the drop due to gravity. You will have to look up the surface
tension of water. |
|
| 2. |
Consider
the "Laplacian operator" 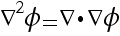 (i.e. the
divergence of the gradient) (i.e. the
divergence of the gradient)
a) Write out the Laplacian of φ in Cartesian coordinates.
b) Using index notation, show that 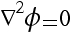 if φ is a "velocity potential" for an irrotational
flow. if φ is a "velocity potential" for an irrotational
flow. |
|
| 3. |
Consider the "water-pressure
car" shown below:
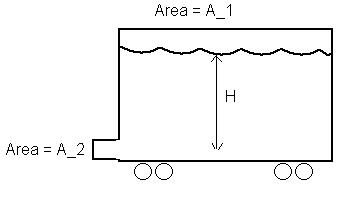
Initially, the depth of the water is H. Assume A1
>> A2 , so the speed of water inside the tank is
small.
a) Find the thrust force as a function of h, the depth of the liquid at
any instant.
b) When all the water has drained out of the tank, what will the speed
of the car be?
|
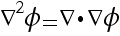 (i.e. the
divergence of the gradient)
(i.e. the
divergence of the gradient)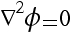 if φ is a "velocity potential" for an irrotational
flow.
if φ is a "velocity potential" for an irrotational
flow.