Physics CS 33	Set # 4
Spring 2006
Due date	Wed. May 3rd
Read HR&K:	Chapter 21 Chapter 23
Read K&K:	None
HR&K Problems:	Chapter 21  Problems 1,  16 Chapter 23  Problem 18 Chapter 24  Problem 9, 10
K&K Problems:	None
1.	Imagine a random process (coin, dice, etc.) with N possible microstates.  The system starts in a "fair" macrostate with each microstate having equal probability (1/N). a) Find the entropy 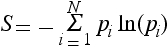  of the system. b) The system undergoes a change which causes the probability of one microstate to increase by a small  amount Δp1 , while another microstate decreases in probability by amount Δp2.   Show that a first order Taylor series for ΔS predicts that the entropy will not change. c) Show that a second order Taylor series for ΔS predicts that the entropy will decrease. d) What could you do to an ideal gas that would make the velocity distribution more closely resemble the "fair" macrostate?
2.	The expansion of a monatomic ideal gas (N particles) is resisted by the weight of a block (mass M, cross-sectional area A).  The system begins in equilibrium with the block at height z0.  Assume the walls and the block transmit no heat, i.e. the total energy of the system is constant. a) What are the pressure and temperature of the gas in its initial state? (Ignore the variation of pressure due to depth in the gas.) b) In an experiment, the top half of the block is slowly removed (one thin layer at a time) and the reaction of the gas is observed.  Find the pressure and temperature of the gas as a function of z, the height of the block.  Assume the mass removal is slow enough that the block has negligible speed at all times. c) In another experiment, the top half of the block is quickly removed and the reaction of the gas is observed.  Find the pressure and temperature of the gas as a function of z, the height of the block.   d) For each experiment (part b and part c), what is the greatest height reached by the block?  To solve one of these equations, you will have to use graphical methods or some trial-and-error on your calculator.
3.	Assuming an infinitely tall atmosphere with one type of molecule (with mass m) at constant temperature, use the Boltzmann factor to write the density of air a distance z above a flat piece of ground (the density at ground level is ρ0).  Show that the force exerted by the air on a piece of ground is equal to the weight of the column of air "sitting" on that piece of ground.
4.	Many different types of energy are proportional to a degree of freedom squared (e.g. (1/2)mvx2 , (1/2)kx2 , and (1/2)Iω2).  The "Equipartition Theorem" states that energy will be equally divided among these degrees of freedom.  Assume that the probability of microstates is described by Boltzmann statistics, and that the temperature of the system is T. a) Show that for a general degree of freedom u  (with energy  E = a u2 ), the expectation value of the energy per particle is given by <E> = (1/2)kT , regardless of what the degree of freedom is.  Hint: You must integrate over all values of the degree of freedom itself, not the energy. b) Based on this theorem, what is the heat capacity per particle in a solid lattice?  Look in HRK to verify this prediction. c) The Equipartition Theorem works well in classical physics but not quantum systems.  Imagine a system with only two possible energy levels, +E0 and -E0  (rather than a continuum).  Again using Boltzmann statistics, calculate <E> per particle. d) Find the heat capacity of this quantum system per particle.
5.	A gas at temperature T consists of N monatomic particles in an infinite space (no walls).  Each particle is attracted to the origin by a spring-type force of magnitude F = B r.  a) Find the distribution function f(r) for the distance of particles from the origin. b) Find the expectation values <x>, <x2>, <r>, and <r2>.  Hint: you can avoid doing the integrals for some of these by using other arguments. c) Find the heat capacity CV for this system.
6.	A gas in a cubical container at temperature T has the Maxwell-Boltzmann speed distribution.  A tiny hole is drilled in the container, and particles are allowed to leak out.  The hole is small enough that the speed distribution inside the box is unchanged.   a) Find the speed distribution function for the particles leaving the hole.  Hint: are all particles in the box equally likely to hit the hole in a given time? b) Show that the average kinetic energy of particles leaving the hole is 2kT.