Set #5

Physics CS 33	Set # 5
Spring 2006
Due date	Wed. May 10th
Read HR&K:	None
Read K&K:	Chapter 11 Chapter 12

HR&K Problems:	None
K&K Problems:	Chapter 12 Problem 12.2 (there is a typo: use t' = 1 sec instead) , 12.3, 12.4

1.	Two masses (2M and M) approach each other, each moving at speed v₀ in the "lab frame". They collide and stick together. Use Newtonian physics in this problem. a) Find the final speed of the combined object in the lab frame. b) Using the Galilean Transformation, find the velocities before and after the collision in the "rest frame" of the mass 2M. Is momentum conserved in this frame? c) Show that the kinetic energy loss in the collision is the same in the lab frame as in the "center-of-mass frame". d) Consider these two events: Event 1: mass 2M's location, 1 second before impact Event 2: collision of two particles Calculate the "distance" (in 4-Dimensional spacetime) between these two events in the lab frame and the center-of-mass frame. Is this distance invariant using the Galilean Transformation?

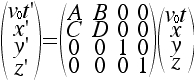
2.	A general Lorentz Transformation corresponding to a boost in the x-direction is of the form: Notice that we have assumed the origins of the two coordinate systems coincide at t = 0 and t' = 0. a) Solve for B, C, and D in terms of A by requiring that the length of the 4-Dimensional position vector is invariant. Your answers will have "plus-minus" ambiguity. b) Since the x and x' axes correspond to the same line in space, D must be positive. What does this imply about the signs of B and C? c) If the origin of the S' frame (i.e. x'=0) moves in the positive x-direction (as viewed by the S frame), determine the correct choice of signs for all terms in the matrix. This is the convention normally used in special relativity. d) Show that a boost in the positive x-direction followed by a boost in the negative x-direction has no net effect.

3.	Einstein's major contribution to special relativity was the postulate that the speed of light through empty space should be constant in all reference frames. Start with the general Lorentz Transformation you obtained in problem 2 c). a) Consider a small wave pulse of light emitted from the origin traveling along the x-axis in the positive direction. Write out the 4-dimensional position vector for this pulse in each frame (S and S'), if Einstein's postulate is correct. b) Use the resulting system of equations to solve for A and v₀in terms of c.

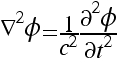
4.	The Lorentz Transformation (LT) gives x' and t' in terms of x and t, and vice versa. In this problem, use the "completed" special relativity version of the LT (the one with the speed of light in the equations). Show that these relationships are consistent by plugging the inverse LT (that is, x( x' , t') and t( x' , t' ) ) into the LT (that is, x' ( x , t ) and t'( x , t ) ).

5.	Electromagnetic waves obey a similar wave equation to other waves. The 3-dimensional version of the wave equation is: where φ is a scalar function of space and time. a) Consider a frame S' moving at speed V relative to frame S. Using the chain rule and the inverse Lorentz Transformation, evaluate the derivatives: 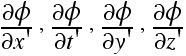in terms of derivatives in the S frame. b) Show that the wave equation above holds for derivatives taken in any reference frame.

6.	Observer A, in a spaceship which passes the Earth at speed 0.6c, synchronizes its clock with observer B on the ground, such that their origins coincide when t = 0 and t' = 0 (that is, we can use the usual form of the Lorentz Transformation). The spaceship then begins to emit light pulses every 1 second, as measured in its own frame. a) Draw a spacetime diagram showing the spaceship and the light pulses it emits traveling back toward Earth. b) How much time elapses on Earth between the received pulses? c) Every time a light pulse reaches Earth, Observer B sends a response light pulse to the spaceship. The spaceship continues to emit pulses every 1 second (in its own frame). How much time elapses between the received pulses at the spaceship?

7.	a) A 2-dimensional coordinate system S (coordinates: ( x, y ) ) is rotated counter-clockwise by an angle θ to produce S' (coordinates: ( x' , y' ) ). Write out the 2 x 2 rotation matrix that describes the relationship between ( x', y' ) and ( x, y ). b) Write out the Lorentz Transformation for the 2-D vector ( ct, x ) as a 2 x 2 "rotation" matrix. What do you notice about the signs of the off-diagonal elements compared to those in part a? c) Draw the x, x', ct, and ct' axes for a typical spacetime diagram. Describe how this is consistent with the matrix from part b.