a) As measured by another reference frame, will the total energy of the system be greater, less, or the same compared to the total energy measured in the lab frame? Explain your reasoning.
b) The two photons collide to produce an electron / positron pair. If the electron has a KE equal to its mass energy (in the lab frame), calculate f0, the frequency of each photon before the collision.
c) Would you imagine that pair production from photon/photon collisions takes place often in the core of the Sun? Explain your reasoning.
d) Today's universe contains a mix of photons and matter, with lighter particles being more abundant than heavier ones. Qualitatively explain how this observation supports the Big Bang theory of a very hot early universe.
b) Imagine a star in the Milky Way galaxy, on the opposite side of the Galactic Center from the Sun. As viewed from the solar system, this star would have a velocity which is perpendicular to the line-of-sight to the star (due to the rotation of the galaxy).
If the star's spectrum contains an absorption line at frequency f0 and the relative speed of the Sun and the star is V, find the observed frequency of the absorption line. Ignore any obstructions in between the two, and the relative velocity of Earth and Sun. This is called the "Transverse Doppler Shift".
c) For two distant observers with a given relative speed V, find the angle between the velocity vector and the line-of-sight which results in zero Doppler shift.
a) Consider such a reaction in which the deuteron and proton barely overcome their electric repulsion, and have negligible remaining KE when they collide. Look up the rest masses of the reactants and products, and compute the energy of the photon produced (as measured in the center-of-momentum frame).
b) What fraction of the original mass energy is converted to photon energy in this process?
a) Solve for ( v / c ) in terms of z.
b) Light from a distant galaxy is observed with a redshift parameter z = 5. Assuming a Hubble constant H0 = 70 (km/sec) / Mpc, calculate how long ago the observed photons were emitted from this galaxy.
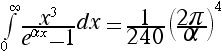
b) The total power radiated from the surface of the Sun is 3.8 x 1026 Watts. Use this and your answer from a) to estimate the surface temperature of the Sun.
a) Imagine a collision which occurs a distance r away from the center of the Sun. The photon collides with an electron and scatters at angle θ, then travels a distance d, where it has another collision, this time at distance r + Δr from the center of the Sun. Using the law of cosines, estimate Δr in terms of the photon scattering angle θ. Assume Δr << r .
b) If the probability of a particular θ is evenly distributed over all possible values, estimate the expectation value <Δr > between two collisions.
c) Using your answer from part b), estimate the amount of time required for a photon to travel from the center of the Sun to the surface. Assume d = 1 cm.