Pull the string to the right and the drum rolls to the right. Pull the string straight up and the drum rolls to the left. Pull the string at the right angle between these two extremes and the drum does not roll, but slides, to the right (vide infra).

(Thanks to Prof. Harry Nelson for help with the analysis.)

As we can see from the photograph above, the central part of the drum has a smaller diameter than that of the discs between which it is sandwiched, and its diameter is smallest in the middle, where the string is wrapped around it. As noted above, if you pull the string horizontally, the drum rolls in the direction in which you are pulling, and if you pull the string vertically, it rolls in the opposite direction. Between these two directions, you will find an angle at which when you pull the string, the drum does not rotate, but instead slides in the direction of the horizontal component of the force you are applying to the string.

There is more than one way to analyze the behavior of this sytem. The diagram below will help.

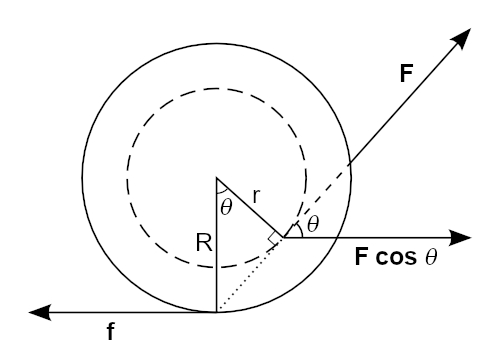
The smaller, dashed circle represents the groove in which the string lies, and the larger, solid circle is one of the rims on which the drum rides. F is the force you apply at the end of the string, f is the force of friction between the rims and the table surface, θ is the angle, with respect to the horizontal, at which you pull the string, and F cos θ is the horizontal component of the force you apply. (The line of force F is dashed within the diameter of the rim, because the string is hidden by it.) R is the radius of the rims, and r is the radius of the inner part of the drum where the string lies.

A simple way to approach this system is to note that when you pull the string horizontally to the right, the line of force intersects R at the inner circle, and it exerts a clockwise torque about the point where the rim makes contact with the table, which rotates the drum in the clockwise direction, toward the right. If you pull the string upward, you exert a counterclockwise torque about the other end of r, in turn exerting a counterclockwise torque about the contact point, and the drum rolls to the left.

In order for the drum to roll, there must be a net torque about the contact point, which acts as a pivot. If you pull the string at some angle, as long as the contact point does not lie on the line along which you are pulling, the force you apply has some moment about the contact point, and the drum rolls in whichever direction that moment acts. If, however, you pull along a line that goes through the contact point, it is impossible for you to exert any torque about that point, and the drum slides. This situation is shown in the diagram; a dotted line extends from the radius at which the string acts, to the contact point. If the line along which you pull passes above the pivot point or goes through the table to the left of it, the drum rolls to the right. If the line along which you pull passes under the pivot point or goes through the table to the right of it, the drum rolls to the left.

Another way to analyze the system is to derive the angular acceleration of the drum about its central axis in terms of F, f, θ, R, r, M and I, where M is the mass of the drum, I is its moment of inertia, and the other variables are as described above. We start with the equation for the no-slip condition (rolling without sliding), which relates the angular acceleration of the drum to its horizontal acceleration:

Rα = a

For the purposes of this analysis, we take acceleration to the right as positive, which means that rotation in the clockwise direction is positive. For the horizontal acceleration, then, we have:

Ma = F cos θ - f

(Friction exerts a force to the left.) The torque is:

Iα = -Fr + fR, or (I/R)α = -F(r/R) + f

(Friction exerts a clockwise torque, whereas the force on the string exerts a counterclockwise torque.) Substituting the first equation into the second gives:

MRα = F cos θ - f

Adding this to the equation above gives:

(MR + I/R)α = F(cos θ - r/R)

from which we see that the angular acceleration of the drum is:

α = F(cos θ - r/R)/(MR + I/R)

This equation is interesting in two ways. First, even though friction opposes both the torque and the horizontal force exerted by the string, it does not appear explicitly in the equation. Second, we see from the numerator that for all angles where cos θ exceeds r/R, α is positive; the drum rolls to the right. For all angles where cos θ is less than r/R, α is negative; the drum rolls to the left. For the angle whose cosine equals r/R, however, the numerator equals zero; α equals zero, and the drum slides to the right. This angle is shown in the diagram above. We see that this is the angle at which the line of force goes directly through the contact point, as shown by the dotted line in the diagram. There can thus be no torque about this point, and the drum slides without rolling.

We also see that the closer r is to R, the smaller the angle at which the line of force goes through the contact point, and as r decreases, the angle at which the line of force goes through the contact point increases. This also means that the smaller the inner radius is, the greater the angle at which you have to pull the string in order to make the drum roll to the left.

We can find an expression for the friction if we rearrange the second and third equations above and then add them:

f = F cos θ - MRα, or f/MR = (F cos θ/MR) - α

and

f = (I/R)α + F(r/R), or f(R/I) = F(r/I) + α

to give

f(1/MR + R/I) = F cos θ/MR + F(r/I)

Dividing both sides by (1/MR + R/I) and collecting terms gives

f = F[(I/R) cos θ + rM]/(MR + I/R)

As we would expect, we see that the friction depends on the angle at which you pull the string. All other things staying the same, for a horizontal pull, cos θ equals one, and friction is at its maximum value. For a vertical pull, cos θ equals zero, and friction is at its minimum value. Relative to horizontal, the smaller the angle at which you pull, the greater the friction, and the greater the angle, the smaller the friction, until you reach the minimum at 90°. When you pull the string at the angle at which the line of force goes through the contact point, when you overcome static friction, the drum begins to slide, and the friction is now kinetic friction. When this happens, the force you must exert to keep the drum sliding is somewhat smaller than the force it took to overcome static friction. If you want the drum to keep sliding without rolling, you must maintain the angle so that the line of force always goes through the contact point.