By placing your hand on top of the book, and exerting a horizontal force directed away from the spine and perpendicular to it, you can illustrate the action of a shear force.

A force applied parallel to the plane of cross section of a material, or to the plane of the interface between two pieces of a material (or such planes within a material) is called a shear force. A force that when applied to an object could deform it is called a stress. If it is parallel to the plane of cross section, it is a shear stress. This bears comparison to a normal stress such as that illustrated in demonstration 32.21 -- Stretch wire to breaking point, which is perpendicular to the cross section of the material (and in this case is a tensile stress). In this demonstration, when you press the front cover of the book away from the spine, you apply a horizontal force, parallel to the cover. Friction between the back cover of the book and the table top prevents the book from sliding, and the force you apply causes deformation of the book. These two forces alone should exert a torque about the center of the book. As you press the cover of the book in a horizontal direction, you and the table also exert opposing forces along the spine and the opposite face of the book, which cancel this torque. These forces are shown in the diagram below.

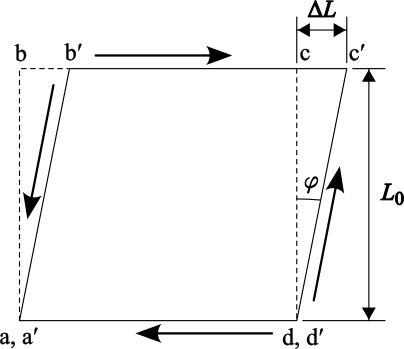
The diagram above is a side view of a block being deformed by shear forces. The original outline of the block is shown by dashed lines. The rightward-facing arrow along the top face of the block represents a horizontal shear force applied there, similar to the force you apply to the front cover of the book when you perform this demonstration. The leftward-facing arrow along the bottom face represents the friction force provided by whatever is supporting the block, which balances the force applied to the top face. This is the friction force the table provides that keeps the book from sliding when you push the front cover. The two arrows along the slanted faces are also generated when you push the top of the book, and as noted above, prevent the book from rotating under the horizontal forces.

We notice that as the block deforms, the lengths of the four faces shown remain nearly the same, but the material parallel to the diagonal plane b-d/b′-d′ is compressed while that parallel to the plane a-c/a′-c′ is stretched. (Note that the components of the forces shown point inward along diagonal b-d/b′-d′, and outward along diagonal a-c/a′-c′.) The deformation, or shear strain (or shearing strain), is defined as the tangent of the angle φ shown in the diagram, which equals ΔL/L₀, the distance by which the top surface is shifted divided by the initial height of the block, and which for small angles approximately equals φ.

For objects under (normal) tensile or compressive stress, the strain is related to the stress by the Young’s modulus of the material, usually denoted Y. This is a measure of the elasticity of the material, and in engineering contexts, it is usually called the modulus of elasticity, and denoted E. It is the ratio of the stress to the strain:

Y = (F/A)/(Δl/l₀)

Where l₀ is the original length of the material, and l is the length of the material when it is stretched or compressed. (See demonstration 32.21 -- Stretch wire to breaking point.) Similarly, when an object is subject to shear forces, the resulting deformation is given by the shear modulus, the ratio of the shear stress to the shear strain, which is usually denoted G (and sometimes denoted S):

G = (F/A)/(ΔL/L₀) = (F/A)/φ

F is the horizontal force applied to the top surface of the block (or that you apply to the front cover of the book), and A is the area of the top surface of the block (or the front cover of the book). For most materials, the shear modulus, G, is typically one half to one third the size of the Young’s modulus.

 

References:

1) Sears, Francis Weston and Zemansky, Mark W. College Physics, Third Edition (Reading, Massachusetts: Addison-Wesley Publishing Company, Inc., 1960), pp. 205-210.
2) Giancoli, Douglas, C. Physics: principles with applications, Fifth edition (Upper Saddle River, New Jersey: Prentice-Hall, 1998), pp. 253-257.