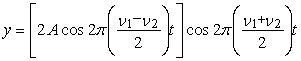A video of this demonstration is available at this link.
The original page for this demonstration showed two tuning forks, both tuned to 266 Hz, clay and a mallet, and no oscilloscope. You can, of course, perform the demonstration in the original way if you wish. The three tuning forks in the photograph, from left to right, sound at 256 Hz, 266 Hz and 266 Hz, respectively. (256 Hz is, by the obsolete “physics standard,” middle C. According to the modern musical standard for an equally-tempered scale in which A = 440 Hz, middle C is 261.63 Hz.) Whichever way you use the demonstration, you must use the hard-wired house microphone, placed near the opening of the resonating box of the middle tuning fork (or, if you use only the two 266-Hz forks, between the openings of their boxes), so that the class can hear the tones.
The idea of this demonstration is to illustrate the beats that occur when one sounds two tones that are close in frequency to each other, but not exactly the same frequency. When you sound the two tuning forks that are tuned to 266 Hz, the class hears a pure tone. When you press a small lump of clay onto one of the tines of one of these tuning forks, the added mass lowers its frequency somewhat. How much lower depends on how much clay you add. When you then strike both of the 266-Hz tuning forks, you hear beats having a frequency equal to the difference in their frequencies. With the small lumps of clay in the plastic tub, you can vary the beat frequency from about 0.5 Hz to around 10 Hz.
When you strike the 256-Hz tuning fork and then one of the 266-Hz forks, this generates beats at 10 Hz. Though Resnick and Halliday state that one can detect beats by ear up to a frequency of about seven Hz (Resnick, Robert and Halliday, David. Physics, Part One, Third Edition (New York: John Wiley and Sons, 1977), p. 445), my impression is that these 10-Hz beats are fairly obvious.
The main point of this demonstration is for the class to hear the beats. It may be desirable, however, for the students also to have a visual display of what is happening to cause the beats. This is the purpose of the oscilloscope, which in the photograph above is showing the 10-Hz beating between the 256-Hz and 266-Hz tuning forks. The oscilloscope also does a good job of displaying the 1-to-2-Hz beats that occur with the two 266-Hz forks prepared as described above. To do this, it may be necessary to change the time base setting by one or two steps, but this is quick and easy to do. The oscilloscope also has an XGA port that connects to the data projector in each lecture hall, so you can easily make the display visible to the whole class.
What is happening:
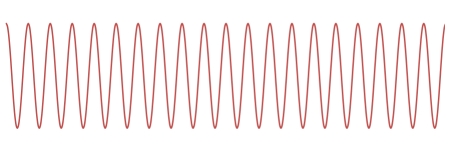
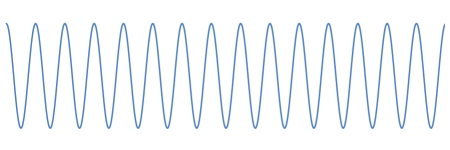
Beats are a phenomenon caused by the superposition of two waves that have slightly different frequencies. These waves can be of any shape, and they do not have to be the same amplitude, but the case of two sinusoidal waves of equal amplitude makes a good illustration. Below are two sinusoids, the one on top having 20 cycles and the bottom one having 15 cycles. If we take the length of the plots as corresponding to one second, then these represent two waves, one of 20 Hz and one of 15 Hz.
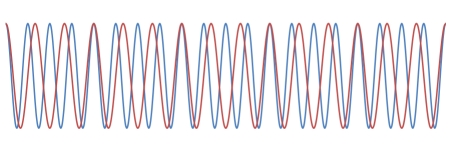
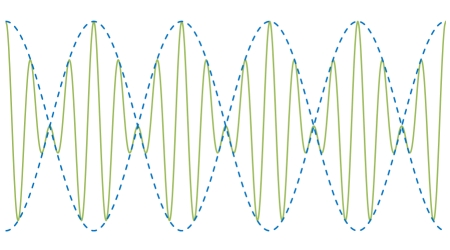
Below, at left are the two waves superimposed on each other. You can see that because of their different frequencies, at some points they are in phase, and at some points they are out of phase. The graph on the right is the sum of the two waves, with dashed lines showing the envelope of the resulting wave. The peaks correspond to places where the waves are in phase, and the nodes occur where they are out of phase.
→ In the wave on the right, there are now five maxima in the same time span in which there were 20 and 15 in the two original waves. If we call the frequencies of the two individual waves ν1 and ν2, for a particular point we can express the displacements produced by the waves as y1 = A cos 2πν1t and y2 = A cos 2πν2t, respectively (where A = ymax). The superposition of the two waves gives the resultant displacement as y = y1 + y2 = A (cos 2πν1t + cos 2πν2t). Because of the way cosines add, this can be written:
The resulting wave thus has a frequency of (ν1 + ν2)/2, the average of the two individual frequencies, and the amplitude factor is now the quantity in brackets, which varies with a frequency of (ν1 - ν2)/2. A maximum in amplitude occurs whenever cos 2 π((ν1 - ν2)/2)t = 1 or -1. Since each of these values occurs once per cycle, the beat frequency is twice the term in parentheses, or ν1 - ν2, the difference between the frequencies of the two individual waves. Hence the 5-Hz beat in the example above for the sum of a 20-Hz wave and a 15-Hz wave.
If the frequencies of two waves are far apart, their sum merely results in a complex waveform, in which the higher-frequency component “rides on” the lower-frequency one. If the frequencies are close, but both relatively high, the beats can occur at high frequencies. The production of audio-frequency beats from two radio-frequency oscillations is the basis of an electronic instrument called the theremin.
References:
1) Berg, Richard E. and Stork, David G. The Physics of Sound (Englewood Cliffs: Prentice-Hall, Inc., 1982), pp. 223, 228.
2) Resnick, Robert and Halliday, David. Physics, Part One, Third Edition (New York: John Wiley and Sons, 1977), pp. 419-420, 444-445.