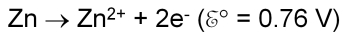One probe of a galvanometer is hooked to a piece of copper, the other probe to a piece of zinc-plated steel. When you place the metals in a Petri dish and fill the dish with distilled water, the galvanometer shows no current flow. When you add drops of dilute acid to the water, the meter registers a current.
This is a simple electrochemical cell, specifically a galvanic cell or a voltaic cell. In a galvanic (or voltaic) cell, coupled oxidation and reduction reactions (often called ‘redox” for short) develop a potential difference between the two cell electrodes and can drive an external load. One can also drive coupled redox reactions in their reverse directions by applying an external voltage across the cell, in which case it is called an electrolytic cell. Examples are the recharging of (rechargeable) batteries, electrochemical production of certain metals, and electroplating. This demonstration shows in a qualitative way the the conversion of chemical energy to electrical energy in a galvanic cell. The explanation below offers both a qualitative and a quantitative description of what is going on.
A transparency summarizing the reactions below is available for use in class. If you would like to download and print a copy for yourself, you can find a Word file here, a PowerPoint file here and a .pdf file here.
In the cell in the photograph above, the oxidation reaction is:
The reduction reaction is:
The hydrogen ion in this reaction comes from the dissociation of the acid added to the water:
“HA” stands for any protic, or Arrhenius, acid. That is, any acid that in aqueous solution dissociates in the manner shown above to yield one or more protons and an anion. As the first two reactions illustrate, oxidation is the loss of an electron (or multiple electrons), and reduction is the gain of an electron (or multiple electrons). These are called &ldqup;half-reactions,” because one cannot occur without the other. If one species is oxidized, it must have something to reduce, and vice-versa. The overall reaction for the cell, then, is:
The numbers in parentheses, labeled “E°,” are a measure of the tendency for each reaction to proceed as written (vide infra). Because of their differences in nuclear charge and electron configuration, the various elements have different tendencies either to gain or to lose electrons. For example, the alkali and alkaline earth metals easily lose electrons. The halogens and some transition metals are easily reduced. For most transition metals, semimetals, nonmetals and halogens, the tendency to be oxidized or reduced depends on the oxidation state of the element, that is, how many electrons it has already lost. (Most transition metals, semimetals and nonmetals have at least two oxidation states; several have three or more. Chlorine, bromine and iodine have multiple oxidation states.) These tendencies determine for each redox couple whether energy is released in the process, giving rise to an electrical potential across the cell that can drive an external load, or whether an external potential must be applied across the cell to make the reaction proceed.
It is useful to be able to calculate the cell potential for any redox couple, at least for the purpose of designing electrochemical cells to provide current at desired voltages. Since for every redox couple the voltage is the sum of the contributions from both the oxidizing species and the reducing species, and because one cannot separate the two processes, it is impossible to measure directly the potential for either the oxidation or the reduction alone. We therefore need a reference half-reaction, against which to measure all the others. By convention, the reduction of H+, shown above, is this reference, and its potential is arbitrarily set to zero volts. Also, because the temperature and the relative concentrations of the products and reagents affect the tendency of the reaction to go in one direction or the other, these half-cell potentials must be measured under standard conditions, hence the designation “E°.” Standard conditions are 298 K and all concentrations set to 1 m (1 molal, or 1 mole per 1000 g of solvent). For gaseous species, for instance the hydrogen in the half-reaction above, the partial pressure is set to 1 atmosphere. (Some take 1 molar (1 M, or 1 mole per liter of solution) and 1 bar as standard conditions.) All half-reactions so measured are written as reductions. The resulting set of half-reactions arranged in order of standard reduction potential, descending from the highest positive potential, passing through zero and then going to the greatest negative value, is known as the electrochemical series. Any reduction will proceed in the forward direction when coupled with a reduction that is below it in the series. Conversely, when a reduction is coupled with one that is higher in the series, it will be driven in the reverse direction, i.e., it will proceed as an oxidation. In other words, a particular species will oxidize anything that lies below it in the electrochemical series, and it will reduce anything that lies above it. Note that the half-reaction for Zn written above is reversed, and that the standard reduction potential for Zn is -0.76 V. For copper, the two half-reactions involving the neutral metal are:
We can see that copper lies above zinc in the electrochemical series, and, thus, that either cuprous (Cu(I)) or cupric (Cu(II)) ion would oxidize zinc, becoming reduced to neutral copper. In the cell shown above, the only components of the cell are a copper strip, a zinc-plated steel strip, water and acid. The copper is already neutral, its reduced form, so it cannot participate in any redox reaction. It merely completes the circuit to allow the electrons from the zinc to flow back into the cell. Hydrogen lies above zinc in the electrochemical series, so when we add acid to the cell, the hydrogen ion thus created oxidizes the zinc according to the reaction shown above, and current flows through the galvanometer. If we added any kind of copper salt instead of the acid, we would also observe a current. In this case, the copper ion would oxidize the zinc, becoming reduced to the neutral metal in the process.
In most electrochemical cells, the actual cell potential is different from the standard cell potential, because not only can the temperature vary, but the concentrations of the reactants and products are usually not all equal to 1 m (or 1 atm, for gases). The (maximum) work that an electrochemical cell can do is equal to its Gibbs free energy, which for standard conditions is:
where n is the number of moles of electrons transferred in the reaction (per mole of reactant or product), F is Faraday&dsquo;s constant, which is the number of coulombs per mole of electrons, or 1.6022 × 10-19 C × 6.0221 × 1023/mol = 96486 C/mol, and E° is the standard cell potential. The right-hand side of this equation is the product of charge and potential, giving units of energy or work (J). For a reaction that is not in equilibrium, the Gibbs free energy is:
where Q, the reaction quotient, equals the product of the concentrations of the products, each raised to the power of its stoichiometric coeffiecient, divided by the product of the reactant concentrations, each raised to the power of its stoichiometric coefficient. By substituting -nFE and -nFE° into the above equation and then dividing each side by nF, we get the Nernst equation:
Setting the temperature to 298 K, inserting the values for R and F and multiplying by the appropriate factor to convert from base e to base 10, we get:
From the Nernst equation we can see that under standard conditions (all concentrations equal to 1 m or 1 atm), Q equals one, its logarithm equals zero, and the cell potential equals the standard cell potential. When Q equals K, the equilibrium constant, that is, when the reaction proceeds until equilibrium has been reached, the second term equals the standard cell potential, and the cell potential goes to zero. Note, also, that the cell potential does not depend on the absolute concentrations of products and reactants — how much material is in the cell, but only on the ratios of their concentrations raised to the appropriate stoichiometric powers. It is the energy per unit charge that the reaction provides to an external circuit, and is a measure of how far the reaction is from equilibrium. What does depend on how much material is in the cell is the total current the cell can provide.
In the electrochemical cell in this demonstration, if we added a zinc salt and a strong acid so that the solution in the cell contained a particular concentration of each, we could adjust the cell potential. If we added a series resistor to make the galvanometer into a voltmeter (or substituted another voltmeter), we could measure this cell potential. Also, as noted above, if we added a copper salt (with no acid), we would also observe a current, and, again, by adding copper and zinc salts in specific concentrations, we could adjust the cell potential.
Any general chemistry textbook should offer explanations of galvanic cells. In writing this note, I leaned heavily on Steven S. Zumdahl, Chemical Principles, Third Edition (Houghton-Mifflin, 1998) and Bruce H. Mahan, University Chemistry, Third Edition (Addison-Wesley, 1975), and a little bit on Ira N. Levine, Physical Chemistry (McGraw-Hill, 1978).