

Though by no means exhaustive, this motley set of crystal models contains several important and useful structures. Below is a description of each model, followed by some notes about crystal structures, which will clarify some elements of those descriptions. Starting in the back row at the left, the models are:
1) Sodium chloride (face-centered cubic, six atoms per unit cell). If you look at only the sodium ions or only the chloride ions, you see that these are arranged in a face-centered cubic pattern, that is, one ion at each corner of a cube, and one at the center of each face. The sodium chloride lattice contains these two lattices interpenetrating each other. The coordination number is six. That is, each ion has six nearest neighbors to which it is attracted. You can also look at this system as a cubic closest packed lattice of chloride ions, with all the octahedral holes filled in by sodium ions (vide infra).
2) Cesium chloride (cubic, two atoms per unit cell). This is, essentially, a system of two interpenetrating cubic lattices, one of cesium ions and one of chloride ions. If you pick either a cesium ion or a chloride ion, it sits in the center of a cube, with eight of the counter ions surrounding it, one at each corner of the cube. The coordination number is thus eight. Some might refer to this structure as being body-centered cubic. Strictly speaking, this is not correct. Whereas cesium chloride has one type of atom in the center of the cube and the other type at the corners, a true body-centered cubic structure has the same type of atom both in the center and at the corners, as happens, for example, with the alkali metals.
3) Zinc sulfide, wurtzite (hexagonal close-packed (vide infra), four atoms per unit cell). This could also be ZnO, which has the same structure as ZnS. In the wurtzite structure, layers of Zn atoms in a hexagonal close-packed structure alternate with layers of S (or O) atoms, also in a hexagonal close-packed structure. The red strings tied one above the other in a sort of diamond pattern, visible on the left side of the model, show the unit cell, which contains four atoms (four eighth sulfur atoms at top and bottom, one sulfur atom inside, four quarter zinc atoms at the edges and one zinc atom inside, for a total of four atoms). The coordination number is four. You can also look at this structure as a hexagonal closest packed lattice of sulfur ions with half the tetrahedral holes filled with zinc ions. Both ZnS and ZnO can also form a face-centered cubic structure, called the zinc blende structure (which, for ZnS, is also called sphalerite). In this structure, the sulfur (or oxide) ions form a cubic closest packed structure, and, again, the zinc ions fill half the tetrahedral holes. The coordination number for this form is also four.
4) Calcite (CaCO3), also called “calc spar” or “Iceland spar” (though calc spar is usually not clear, whereas Iceland spar is; (trigonal) rhombohedral). In this structure, the edge lengths, a, b and c, along the three dimensions of the unit cell are all equal, and the three angles, α, β and γ, among the planes of the cell (i.e., the (obtuse) angle at which the front and back faces of the cell sit with respect to the top and bottom faces, the (obtuse) angle at which the two side faces sit with respect to the top and bottom faces, and the (obtuse) angle at which the front and back faces sit with respect to the sides) are all equal and do not equal 90°. This is similar to the face-centered cubic structure, in which the carbonate ions would occupy all the octahedral holes in a cubic closest packed lattice of calcium ions. Because the lattice angles are all greater than 90°, however, the lattice is distorted, and so is the shape of the octahedral holes. The layers of hexagonally-arranged atoms that make up the cubic closest packed structure are there, but displaced from where they would lie with respect to each other in a cubic lattice. (It is probably because of this hexagonal arrangement of the atoms within their respective layers that some references may list calcite’s structure as “hexagonal.”)
The crystal lattice of calcite resembles a cubic lattice that has been compressed along one body diagonal and elongated along the other three. This reduces the symmetry of the crystal and results in an anisotropy in the electron distribution throughout the crystal. This anisotropy gives calcite an interesting optical property; it is birefringent. In birefringence, or double refraction, the transmitted portion of the light incident on a crystal is refracted in two directions, so that two refracted rays emerge from the exit face of the crystal, instead of only one. Since opposite faces of a calcite crystal are always parallel to each other, both rays exit parallel to the incident beam and, thus, to each other. One of these rays, called the ordinary ray, obeys Snell’s law. For the other ray, called the extraordinary ray, Snell’s law does not hold. Thus, if light enters normal to a crystal face, the ordinary ray passes straight through, but the extraordinary ray exhibits a nonzero angle of refraction, and it emerges parallel to, but displaced from, the ordinary ray. If you rotate the crystal about the ordinary ray (or incident ray), the ordinary ray stays put, while the extraordinary ray moves in a circle about it. Inside the crystal, the ordinary ray always lies in the plane of incidence. For the extraordinary ray, this is true only for particular orientations of the crystal.
There is also another interesting difference between the O ray and the E ray, which is that they are polarized at right angles to each other. The direction of polarization depends on the orientation of the transmitted light ray with respect to the optical axis of the calcite crystal. The optical axis is parallel to the short diagonal of the crystal. (It is also the axis about which the crystal exhibits three-fold symmetry.) If we imagine a plane normal to the crystal face where the light enters, oriented in the direction of the optical axis, the light traveling along the ordinary ray is polarized in the direction perpendicular to this plane. The polarization of the extraordinary ray is in the direction of this plane.
If you place a crystal of calcite over a printed page as shown below in the photograph at left, then, you see double lines of print. The light from the lower letter of each pair is coming straight through the crystal, along the ordinary ray. The light from the upper letter of each pair is traveling along the extraordinary ray, and exits parallel to, but displaced above, that from the lower letter.
If you rotate the crystal, the lower lines stay in place, and the upper lines rotate around them, making a full circle as you turn the crystal through a complete rotation. The optical axis is parallel to the line that runs from the top corner at front to the bottom corner at rear, in the crystal as it sits in the photographs. As the description above would indicate, the light from the lower set of letters is horizontally polarized, and when we cover the crystal with a polarizer whose easy axis points horizontally, we see this lower set of letters, but the upper set disappears. If we turn the polarizer 90°, so that its easy axis is now vertical, the upper set reappears and the lower set disappears. (As you rotate the crystal the planes of polarization of the ordinary and extraordinary rays rotate with it.)
5) This one is actually a mystery. It resembles a cubic lattice, such as that of sodium chloride, but with alternate vertical planes displaced from the others, and alternate horizontal planes similarly displaced. Also, if it is a distorted version of such a lattice, not all the bonds are present.
And in the front row, from left:
1) Triclinic lattice. This is a structure in which the edge lengths, a, b and c, along the three dimensions of the unit cell are all different, and the three angles, α, β and γ, among the vertical and horizontal planes of the cell (i.e., the (obtuse) angle at which the front and back faces of the cell sit with respect to the top and bottom faces, the (obtuse) angle at which the two side faces sit with respect to the top and bottom faces, and the (obtuse) angle at which the front or back face sits with respect to the sides) are all different, and none equals 90°.
2) Graphite (hexagonal sheets). In this form of carbon, the carbon atoms form sheets in which they are covalently bound in a pattern of fused six-membered rings. That is, the carbon-carbon bonds form hexagons, each of which abuts six neighboring hexagons, etc. These sheets are loosely bound in a layered structure, in which they can freely slide over each other. This is why graphite is often used as a lubricant. In the sheets of graphite, the p orbitals of the carbon atoms overlap to form an extensive network of π bonds, in which the electrons are largely “delocalized,” that is, they have considerable mobility. This, and the fact that the π molecular orbitals are closely spaced, so that it does not take much energy to excite an electron from one to another, give graphite its electrical conductivity.
3) Diamond (tetrahedral, modified face-centered cubic). In diamond, each carbon atom is covalently bound to four other carbon atoms in a tetrahedral arrangement, i.e., each atom sits at the center of a tetrahedron, at each corner of which sits one of the four atoms bound to it. This bonding is called network covalent, and it is responsible for diamond’s great strength and extreme hardness. Within this structure it is possible to discern a face-centered cubic unit cell, shown by the yellow outline in the model, which has one carbon atom at each corner, one at the center of each face, and four atoms within the cell. The unit cell thus contains eight atoms (1/8 at each of the eight corners, 1/2 at each of the six faces, plus four). The coordination number is four. The description here reads, “modified,” because the standard face-centered cubic lattice would not have atoms within the unit cell. This structure is actually a pair of interpenetrating face-centered cubic lattices, separated along a body diagonal, by a distance of 1/4 the length of the diagonal. A second model (not shown), in which half the carbon atoms are black and half are blond, might make this somewhat easier to see.
4) Magnesium (hexagonal closest-packed – vide infra, two atoms per unit cell). One can view this structure as having a hexagonal unit cell in the shape of the model in the photograph. That is, the cell bounded by the hexagons formed by the six atoms in the top layer and the six atoms in the bottom layer, containing the three atoms in the middle layer within the cell. Because the atom at each corner of the hexagon belongs to three cells above and below, 1/6 of each atom is within the unit cell. Half the atom in the face of each hexagon is in the unit cell. This gives 1-1/2 atoms on each face plus the three within, for six atoms per unit cell. It is possible, however, to find a smaller repeating unit cell by taking the rhombus formed at top and bottom by three consecutive edge atoms and the center atom of each hexagon. Such a cell represents one-third of the hexagonal cell described above, and contains one of the three atoms in the middle layer. The two atoms at the acute corners of the top and bottom of the cell fall within 12 neighboring cells, and the two at the obtuse corners fall within six. So the top and bottom faces of this unit cell contain 1/2 atom each (2 × 1/12 + 2 × 1/6). With the whole atom from the middle layer, this gives two atoms per unit cell. Because each atom has 12 neighbors, the coordination number is 12.
5) Copper (face-centered cubic (cubic closest-packed – vide infra), four atoms per unit cell). The unit cell of this structure has one copper atom at each corner of a cube, and one in the middle of each cube face. Since each corner atom falls within eight neighboring cells, and each face atom falls within two, each cell contains 8 × 1/8 + 6 × 1/2 = 4 atoms. Each atom has 12 neighbors, so the coordination number is 12.
6) Water ice (hexagonal). Because oxygen’s affinity for electrons is significantly greater than that of hydrogen, a water molecule has a small net negative charge on the oxygen, and equal positive charges on its hydrogen atoms (each equal to half the charge on the oxygen); it is a polar molecule; it has a dipole moment. It thus exhibits a phenomenon called hydrogen bonding, in which each hydrogen is attracted to, and forms a weak bond with, the oxygen of a neighboring water molecule. Though this occurs to a great extent in water in the liquid phase, the molecules in liquid water have enough energy that hydrogen bonds are continually being broken and reformed, the molecules are essentially randomly oriented, and many of them are either not hydrogen bonded, or are only partially hydrogen bonded. As one cools water, the extent of hydrogen bonding increases, and the water molecules begin to adopt a structure that has greater order. When water freezes, the extent of hydrogen bonding reaches essentially 100% (in liquid water near its freezing point, about 85% of the hydrogen bonds are formed), and the water molecules must adopt an ordered structure, in which the oxygen atom on each molecule sits at the center of a tetrahedron, and, through its two hydrogens and its lone pairs of electrons, is hydrogen-bonded to four other water molecules, whose oxygens sit at the corners of the tetrahedron. This forms a structure in which the water molecules are arranged in layers of fused hexagons, which stack so that the hexagons line up above and below those in the neighboring layers. (If they were to line up in a staggered pattern, so that the center of each hexagon lined up above an atom in the layer below, this would result in the cubic pattern in which diamond forms. Ice can form in this structure, but it is metastable and forms only under special conditions. Normal ice is hexagonal.) This results in a decrease in density as you lower the temperature of water from about 4°C to 0°C, which means that water expands as it freezes. If it is confined in a container with no room in which to expand, it can rupture the container. (See demonstration 48.15 – Ice bomb.)
Here is a short note on the basis for many of the structures described above:
If atoms are to pack efficiently, that is, fit together in such a way as to maximize the number of atoms per unit volume, there are specific arrangements in which they can do so. The nature of the particular structure can be influenced by whether or not the atoms are neutral or charged (i.e., they are ions), and whether or not they are the same size. For a single layer of atoms, if they are uncharged and all the same size, the hexagonal closest-packed structure is the densest. If they are charged, this structure is unstable because of the proximity of too many similarly-charged ions to each other, and the ions must adopt the structure of a square lattice, in which cations (positive) and anions (negative) alternate, and their nearest neighbors are all of the opposite charge (i.e., cations have four anions as nearest neighbors, and anions have four cations as nearest neighbors). This is the structure of any plane in the NaCl lattice. In the hexagonal closest-packed structure, each atom has six nearest neighbors as in the layer below, whose atoms are designated “a”:
If we now add a second similar layer, in order that the atoms can pack most closely, its atoms must lie over some of the interstitial spaces between those in layer a (that is, not directly above the atoms). We’ll designate this layer b:
We see that the atoms in the b layer cover half the interstitial spaces in layer a, leaving half uncovered. If we add a third layer, we can do it in either of two ways. One way is to have the atoms line up with those in layer a:
This structure, in which the layers repeat ababa. . ., yields the hexagonal closest packed structure. Alternatively, we could place the third layer so that it covers the spaces in the first layer that were left open by the second layer:
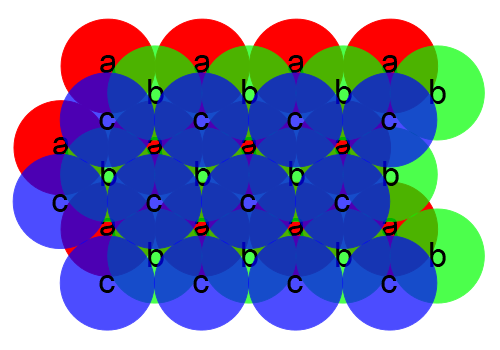
This structure, in which the layers repeat abcabc. . ., yields the cubic closest packed structure. In both of these systems, atoms pack equally efficiently. That is, you can fit the same number of atoms into a given volume. In the hexagonal closest packed structure, we can find the unit cell by drawing a hexagon through six neighboring atoms in an a layer, a similar hexagon in the a layer either directly above or below it, and then connecting the vertices of the two hexagons with vertical lines, enclosing three atoms of the b layer within. We could do the same thing with the second arrangement, enclosing three atoms from the b layer and three from the c layer between the two hexagons in the a layers, but we can find a unit cell that has a higher symmetry, which is face-centered cubic. This system is thus called cubic closest packed, as noted above. Because the hexagonal layers are oriented diagonally with respect to the cubic lattice, this is a bit difficult to visualize, especially with only the two-dimensional diagrams above. The easiest way to see this structure is to take a face-centered cubic lattice and view it from a corner. Below is a sodium chloride lattice, which we can consider as a face-centered cubic lattice of sodium ions interpenetrating a face-centered cubic lattice of chloride ions, as noted above:
In the lattice above, the white balls represent the chloride ions, and the red balls are the sodium ions. The chloride ions have colored dots on them according to the scheme in the two-dimensional diagrams above. The ion at the corner at top front is part of a c layer (blue). Below it, in the next plane of like ions, are six ions in a b layer (green). Below them are the ions in an a layer (red), followed by another c layer, and then by another b layer. In the first a layer, and in the c layer below it, you can see the hexagonal pattern. If you tilt this lattice so that the hexagonal planes are horizontal, the three green-labeled ions nearest the top corner line up with those at the far corner, and the blue-labeled ion at the top front corner lines up with the blue-labeled ion that lies along the diagonal of the cube. If you had a three-dimensional model of a face-centered cubic lattice, made up of closely packed spheres, you could reveal the hexagonal structure by removing the corner atom, then the six atoms in the layer below. You can also see part of this pattern in the copper lattice above. Since this lattice contains only one unit cell, though, you can see only six of the atoms in the a layer (as the chlorine layers are labeled in the NaCl lattice above), in a triangle pointing in the opposite direction to that formed by the six atoms in the b layer.
In the hexagonal closest-packed structure, there are two types of holes – the interstitial spaces among the atoms. If we look at the second diagram above, with layer b covering half the spaces in layer a, the hole under each atom in the b layer (each underneath a letter “b”) is a tetrahedral hole. An atom small enough to fit inside such a hole has four nearest neighbors – one in the b layer and three in the a layer (or vice versa), each at the corner of a regular tetrahedron. (The coordination number for the central atom is thus four.) The other set of holes, where we see white spaces, is a set of octahedral holes. An atom inside such a hole has six nearest neighbors – three in the a layer and three in the b layer. These are at the corners of a regular octahedron. (The coordination number for the central atom is six.) Octahedral holes are larger than tetrahedral holes, and the relative sizes of atoms (or ions) in a system in which one type of atom (or ion) fills holes in the lattice formed by a second type of atom (or ion), determines whether atoms (or ions) of the first type fill tetrahedral or octahedral holes. When the sizes of the two types of atom (or ion) become too close (the radius ratio exceeds 0.732 or is less than 1.37), octahedral holes can no longer accommodate the smaller ion, and the lattice geometry changes. (The limiting radius ratio past which tetrahedral holes become too small to accommodate an atom is 0.414 or 2.42.)
In the lattice above, we can see, as is mentioned in the description above for sodium chloride, that the sodium ions fill octahedral holes; they have six nearest-neighbor chloride ions, each at a corner of an octahedron. (You can find the tetrahedral holes between an ion in one (hexagonal) plane and the three ions in the plane below, for example any of the green-labeled ions toward the front, and the three red-labeled ions in the layer behind it, or any group of three of those green-labelled ions that has one red-labeled ion behind it.) As also mentioned above, in an ionic structure such as this one, the hexagonal closest packed structure is not the most stable arrangment. The presence of sodium ions in the octahedral holes, however, lessens the repulsion among the chloride ions, and although they may not pack exactly in a hexagonal closest packed arrangement (in this case, cubic closest packed), this model still provides a useful approximation.
References:
1) Huheey, James E. Inorganic Chemistry: Principles of Structure and Reactivity, Second edition (New York: Harper & Row Publishers, Inc., 1978), pp. 51-80.
2) Zumdahl, Steven S. Chemical Principles, Third Edition (Boston: Houghton-Mifflin, 1998), pp. 737-744, 759-764.
3) Mahan, Bruce H. University Chemistry, Third Edition (Menlo Park, California: Addison-Wesley, 1975), pp. 90-95, 105-116.
4) Holden, Alan and Singer, Phylis. Crystals and Crystal Growing (Garden City, New York: Anchor Books, 1960), p. 157-159 (calcite structure), 207-209 (glide), p. 235 ff. (calcite birefringence).
5) Jenkins, Francis A. and White, Harvey E. Fundamentals of Optics (New York: McGraw-Hill Book Company, Inc., 1950), pp. 494-498 (calcite birefringence, optical axis, polarizations of O and E rays).