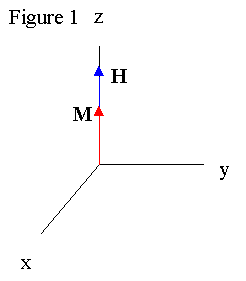
Pulsed nuclear magnetic resonance (NMR) is a powerful and flexible scientific tool which manipulates the magnetic moments µ and angular momentum of atoms to draw conclusions about their local environment. The phenomena can observed in many particles (Magnetic moments of various atoms can be found here ), but is most commonly observed in hydrogen atoms. A sample is placed in a permanent magnetic field B, and dipoles align along the magnetic field because their energy E = -µ . Bo is at a minimum along the field. The net result is a magnetic moment M aligning with the field (See Figure 1).
Once the magnetization aligns, radio waves are directed at the sample, applying a rotating magnetic field H to the net magnetization. The H field rotates in the xy plane, or perpendicular to the permanent magnet field. Magnetizations perpendicular to magnetic fields precess around the field axis, and the precession rate for the atoms is ω = γD, where γ is the atom's gyromagnetic ratio and D is the field strength. The inclusion of H to the sample then rotates M out of alignment with B, and the magnetization precess about H and B fields. The end result is a very complex motion of M which can be simplified in the resonance condition where the frequency of the precession is equal to the frequency of the radio waves. The H and M vectors rotating at the same rate allows us to easily view the situation in a frame rotating at the resonant frequency. In this frame, H is constant, and B isn't observed because of the transformation into a rotating frame. So M can be rotated away from the z-axis by varying the time that H is present, or the duration of the radio pulse (See Figure 2, b) being a time t later than a)).
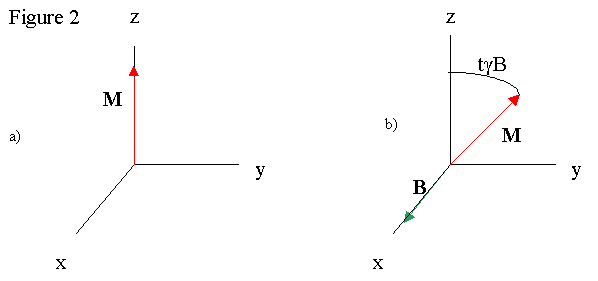
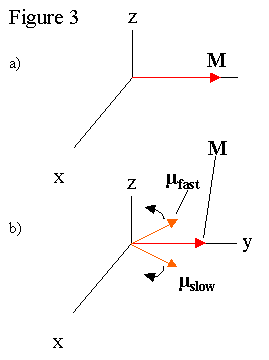
One scientifically interesting position for M to be is perpendicular to B, so the maximum magnetization is precessing about the permanent magnetic field. The radio pulse that rotates the magnetization perpendicular to permanent magnetic is called 90º. In this position, the net magnetization of the sample decreases with time partly because the magnetic field is not constant over the sample. Different local magnetic fields throughout the sample create slightly different B values for each atom, which changes the precession rates for individual µ s. The range of precession rates causes the individual moments to get out of phase, which causes M to decay (See Figure 3). The observation of M decaying is called a Free Induction Decay (FID). If an FID signal is Fourier transformed , the different precession frequencies which drive the FID can be found (see Figure 41). This allows us to back calculate the local magnetic fields at the atoms in the sample, which often elucidates, among other things, the molecular structure of the sample, as in the NMR facility at UCSC . Unfortunately, the equipment in the Senior Lab is not sufficient to study molecular structure in this way, as it requires NMR system with a high homogeniety magnet, such as those offered by Varian Inc. . For some of the basics ideas of structure analysis, please go here .

Pulsed NMR can go beyond molecular structure and analyze molecular interactions. Two of these are the spin lattice relaxation time T1 and the spin spin relaxation time T2. T 1 is calculated by rotating M until it is anti-parallel to H, and observing the behavior of the magnetization. The pulse which rotates M in this manner is called a 180º pulse. The majority of spins are anti-aligned with the permanent magnetic field, so, as the atoms thermally interact, the spins realign with permanent magnetic field. The equation which describes the behavior of the magnetization over time (with t = 0 when the magnetization is rotated) is M(t) = Mo(1 – 2e(-t/ T 1)). For more on the specific techniques used to calculate T 1 and factors which influence it, please go here Go here for research on the Spin-Lattice Relaxation of boron of SrB 6.
The spin-spin interaction is the propensity of oppositely aligned spin pairs to simultaneously flip, which disturbs the phase relationship between the two spins. This causes the magnetic moments of the atoms to dephase much like the varying magnetic field. To study T 2 involves the use of the spin-echo technique, first pioneered by Erwin Hahn . The sample is pulsed with a 90º pulse, then a series of 180º pulses a time τ separated from each other. The 90º pulse rotates the magnetization to the perpendicular plane, where the magnetization begins to dephase as discussed earlier (See Figure 3b). The effect of a 180º pulse causes the magnetizations to rotate out of the plane, and then back into it, essentially reflecting the magnetizations across an axis (See Figure 3c & 3d). Since the magnetizations continue rotating at their relative rates, they rephase momentarily before they begin to dephase again (See Figure 3e & 3f). The 180º pulse can be repeated to get an accurate picture of the decay of the magnetizations, thus sidestepping the issue of dephasing due to magnetic field inhomogeniety. A Meiboom-Gill pulse sequence introduces a π/2 phase shift between the 90º and 180º pulses, which reduces the effect of the 180º pulse not being exactly the correct duration. T 2 is a scientifically interesting quantity because it may help identify diseases and tumors within the lungs . A more complex use of 90º and 180º pulses is the nuclear Overhauser effect , which involves the coupling of electron and nuclear magnetic moments to magnify the nuclear moment.
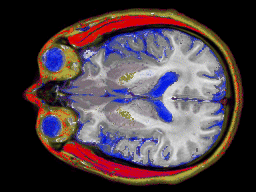
NMR has various practical applications, the most visible of which is magnetic resonance imaging (MRI). MRI is a technique used for imaging sections of the human body by studying the different resonance frequencies under a spatially varying magnetic field. The technique was first demonstrated in organic tissue by Paul C. Launterbur in 1973, and the technique has progressed from a series of two-dimensional pictures (right above2) to also allow volumetric imaging (right below3). MRI is also being applied to non- medical tasks : radiation dosage in gels and flow measurements. For more on the techniques and underlying physics of MRI, please visit here .
As you can see, NMR is important scientific tool for understanding molecular structure and environment, and holds promise for future practical applications. In the coming years, NMR will hopefully expand it application outside the medical and scientific fields to industry, and further enrich our lives.
1. Picture courtesy of Spektroscopy [sic] Online, http://www.chem.uni-potsdam.de/tools/
2. Picture courtesy of Graphics and Visualization Center, http://www.gg.caltech.edu/sitevis/mri_research.html
3. Picture courtesy of Emory University Cardiac MRI, http://www.emory.edu/RADIOLOGY/MRI/FPMRRCb.html