The Zeeman Effect.
Contents
Theory
There are three quantum numbers that are needed to solve the Schroedinger equation for stationary states. They are n,l and m. For atoms with the inner shells filled, or they screen the coulomb potential, the energy of these eigenstates only depends on n and l but not on m. This means that there are degenerate energy states, that is, there are more than one state with the same energy value for that one value of m.
In the presence of an external magnetic field the energy is
changed. The energy of one of these states is given by the equation 
where H is the external field. The angle between L and H is
quantized so it can only take 2l + 1 values. Not a continum of values. For an explanation of
discrete values. The application of the external field lifts the degeneracy
and splits the energy levels. See below.
The far left lines are two energy levels that are
unsplit. They are then split into 3 and 5 lines respectivly in the middle
of the picture when an extenal field is added, field not shown. On the
right the picture shows the allowed transitons. Note all energy spacings are equal, that is a = b.
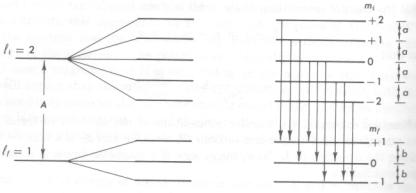
The light that is emitted by these transitions will make spectrum lines when observed. This spectrum is from what is called the normal Zeeman effect.
There is also the Anomolous Zeeman effect. This
arrises when the Magnetic moment of the electron is taken into effect. The spin
angular momentum of the electron S is
coupled to the Angular momentum by the relation J = L + S. The
consequence of this is that the energy levels
now are not equidistant. Now the energy levels are given by the equation
where g is the Lande
g factor. For an
explanation of this energy The
result of this equation is that now the energy is dependant on (gμH) which
is constant, but also in mj which is no longer constant. This
results in more lines and lines that are not of the same energy.
For lines see picture below.
On the left is the Normal Zeeman effect. The one line is
split into three when an external field is added. On the right is the Anomalous Zeeman effect that takes
electron spin into account.
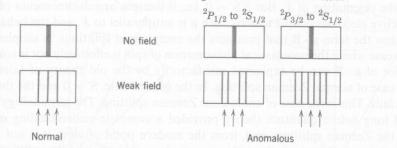
One interesting fact about the Zeeman effectg is that the light has differing polarization depending on wheather it is viewed parallel to or normal to the external magnetic field. When viewed parallel to field the light is linearly polarized. When viewed normal to field the light is circularly polarized.
See picture below.
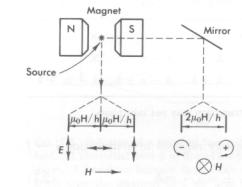
For explanation and experimental setup
Interesting and Helpful Links
Another good theory
explanation and experimental setup
For how Zeeman is
used in astronomy
For how Zeeman is used
in Atomic Spectra
Paper on use of
Zeeman in stellar CN cloud investigation
How Zeeman is used
to investigate stellar magnetic fields
Paper on OH stellar
cloud investigation