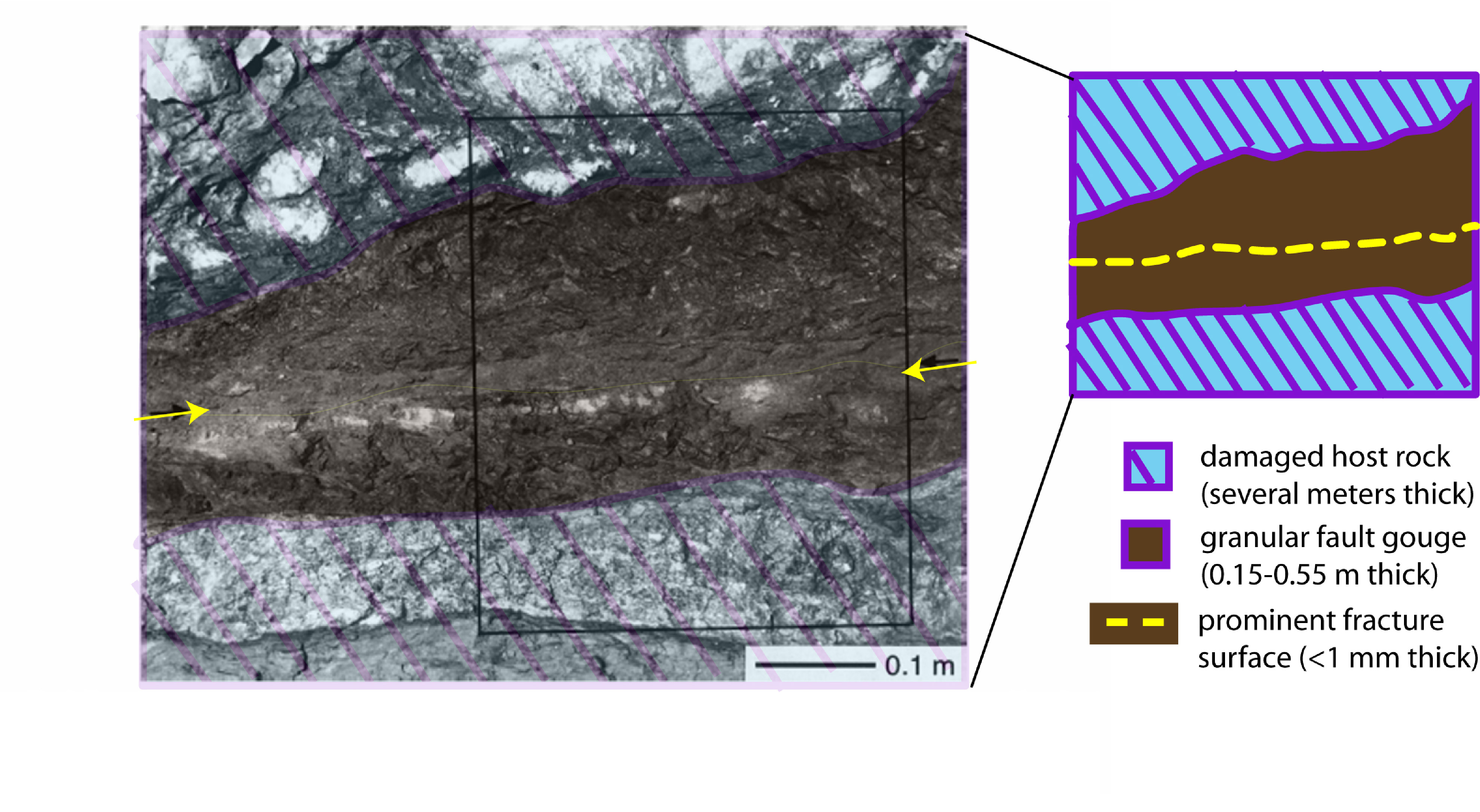
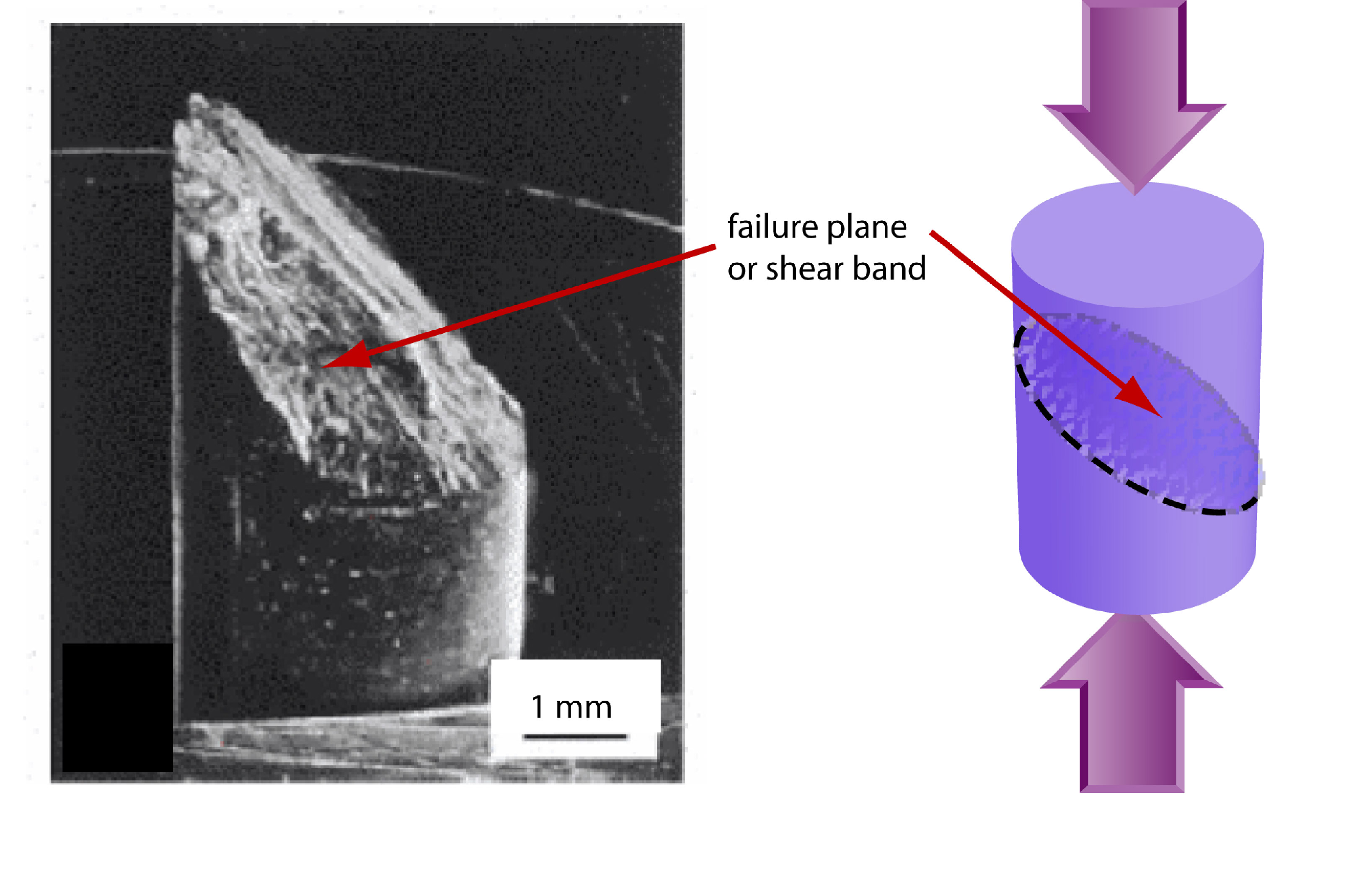
What is an amorphous material?
Although ruptures on earthquake faults, nanoscale friction measured using a Surface Force Apparatus, and deformation in bulk metallic glasses appear to be very different phenomena, they share a common feature: the region where deformation or slip occurs is populated by an amorphous material. Amorphous solids are comprised of particles (atoms, grains, bubbles, molecules) arranged so that the locations of their centers of mass are disordered; their structure is essentially indistinguishable from a liquid. However, these materials are ``jammed'' and exhibit a yield stress like a solid. Other examples of amorphous materials include colloids and emulsions, foams, glass-forming molecular liquids, traffic jams, and even living tissue.

While amorphous materials differ in important and significant ways, they exhibit common features which we explain using a single continuum formalism. One such feature is a mode of deformation or failure called shear banding or strain localization. Strain localization is the spontaneous development of coexisting flowing and stationary regions in a sheared material.
 Amorphous materials
Amorphous materials