Econophysics

  • Recently, members of the Carlson group have begun to study economic systems. Robustness and tradeoffs are clearly integral to these complex systems, which are characterized by large interconnected networks, specialization, and catastrophic failure.
  • Back to research page

Stochastic Portfolio Theory

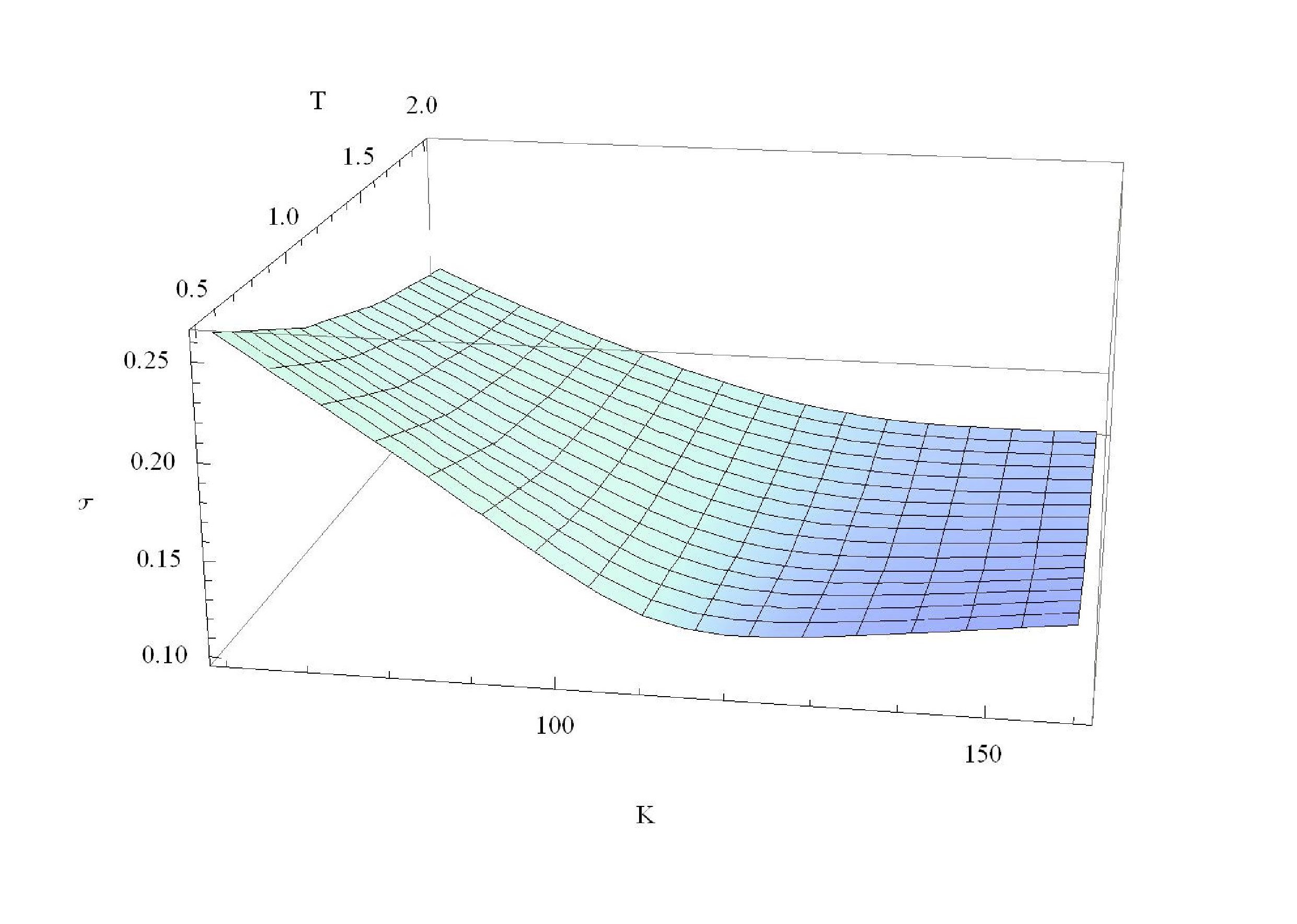
We study optimal strategies for portfolio management with respect to various objectives, constraints and market models. We are particularly interested in low information approximations to the portfolio known as growth-optimal, numeraire or Kelly under real world market frictions. Additional information about the hidden market parameters will increase the growth rate of the approximated numeraire portfolio, so quantification of the value of information is a goal.

We are also looking at incorporation of previously ignored catastrophic risks into traditional financial models. For example, in continuous market models the risk of an individual stock crashing to zero is usually omitted, not to mention the risk of an entire market crash. Does incorporation of these ignored risks into existing models qualitatively alter their characteristics? Is it desirable to ignore these risks in modeling or should we be using models with catastrophe built in?

Questions? Email Winslow Strong

Volatility

Volatility is a measure of how uncertain the future price of a given stock is. In the Black-Scholes option pricing formalism, volatility of the underlying stock is assumed to be constant in time. This assumption produces log-normal transition densities for stock prices. However, empirical evidence shows that the transition densities for real stocks are not log-normal. As such, the Black-Scholes formula misprices options.

One way to address this issue is to allow a stock's volaility to vary randomly in time. Models that do this are referred to as stochastic volatility models. My research focuses on the volatility process itself. What sort of process does volatility follow? How are option prices affected by the volatility process? These questions are important to answer in order to understand the dynamics of the stock market.

Above: A plot of the implied volatility surface produced by the Heston Model--a popular stochastic volatility model. Option prices are first calculated using the Heston model. Then, the implied Black-Scholes volatililty is plotted as a function of strike price a maturity.

Questions? Email Matt Lorig.