The No-Boundary Wave Function

Predictions

Contemporary final theories have two parts --- a theory of dynamics (H) like superstring theory, and a theory of the universe's quantum state (\Psi) like the no-boundary wave fun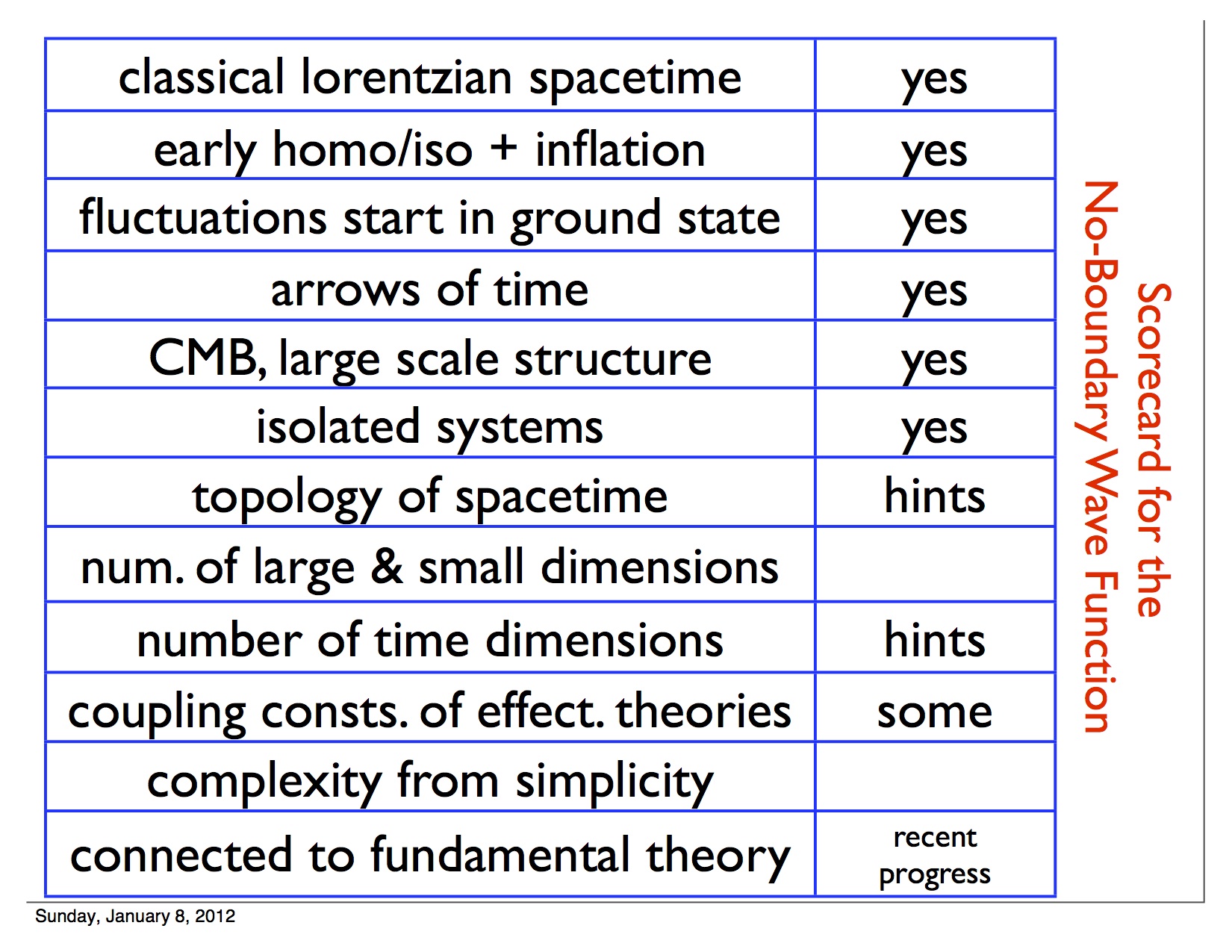ction. Every prediction in principle involves both. But some features of our universe depend more on one than the other. Regularities in time arise mostly from H; regularities in space arise mostly from \Psi. Of particular importance are the predictions of \Psi for the probabilities the large scale classical spacetime geometry of the universe. Most cosmological observations are of properties of that classical spacetime or follow from it. What is the probability that our universe inflated in the past? What is the probability that it is approximately homogeneous and isotropic now? What is the probability for our observations of the galaxy distribution and for the CMB? What are the probabilities for our observations of the cosmological constant if its value differs from place to place? The papers in this section are devoted to how the NBWF answers such questions.

More features of the universe for which \Psi are in the slide at righttogether with the status of their prediction by the NBWF as of 2012. The slide is from the author's talk at the Hawking 70th birthday celebration.

 

The No-Boundary Measure of the Universe [139]
Classical Universes of the No-Boundary Quantum State [140]

(with S.W. Hawking and T. Hertog) We analyze the predictions of the NBWF for classical spacetimes in a class of minisuperspace models. These assume homogeneous, isotropic, closed spacetime geometries, a single scalar field moving in a quadratic potential, and a cosmological constant. The allowed classical histories and their probabilities are calculated to leading semiclassical order. Probabilities are derived for whether the histories are initially singular or bounce at a small radius, for whether they expand forever or recollapse, and for the amount of scalar field inflation in the universe we observe. The first paper is a `letter' summary; the second has all the details.

The No-Boundary Measure in the Realm of Eternal Inflation [145]

(with S.W. Hawking and T. Hertog) This paper explores the predictions of the NBWF for linear scalar fluctuations about homogeneous and isotropic backgrounds in models with a single scalar field moving in a quadratic potential. Both the spacetime geometry of the universe and the observers inhabiting it are treated quantum mechanically. We evaluate probabilities for local observations that are conditioned on the NBWF and on part of our data as observers of the universe. For models where the most probable histories do not have a regime of eternal inflation, the NBWF predicts homogeneity on large scales, a specific non-Gaussian spectrum of observable fluctuations, and a small amount of inflation in our past. By contrast, for models where the dominant histories have a regime of eternal inflation, the NBWF predicts significant inhomogeneity on scales much larger than the present horizon, a Gaussian spectrum of observable fluctuations, and a long period of inflation in our past. The absence or presence of local non-Gaussianity therefore provides information about the global structure of the universe, assuming the NBWF.

Local Observation in Eternal Inflation [146]

(with S.W. Hawking and T. Hertog) We consider landscape models that admit several regions where the conditions for eternal inflation hold. It is shown that one can use the NBWF to calculate small departures from homogeneity within our past light cone despite the possibility of much larger fluctuations on superhorizon scales. The dominant contribution comes from the history exiting eternal inflation at the lowest value of the potential. In a class of landscape models this predicts a tensor to scalar ratio of about 10%. In this way the no-boundary wave function defines a measure for the prediction of local cosmological observations.

next page