SUPERSTRINGS! Black Holes

The classical description of gravity known as General Relativity, contains solutions which are called "black holes". There are many different kinds of black hole solutions but they share some common characteristics. The event horizon is a surface in spacetime which, loosely speaking, divides the inside of the black hole from the outside. The gravitational attraction of a black hole is so strong that any object that crosses the event horizon, including light, can never escape out of the black hole. Classical black holes are therefore relatively featureless, but they can be described by a set of observable parameters such as mass, charge, and angular momentum.

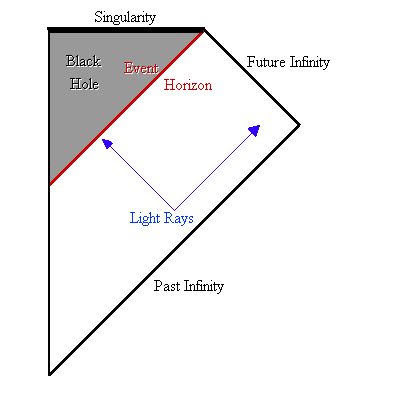
Penrose diagram of a black hole (explanation of this Penrose diagram)

Black holes turn out to be important "laboratories" in which to test string theory, because the effects of quantum gravity turn out to be important even for large macroscopic holes. Black holes aren't really "black" since they radiate! Using semi-classical reasoning, Stephen Hawking showed black holes emit a thermal spectrum of radiation at their event horizon. Since string theory is, among other things, a theory of quantum gravity, it should be able to describe black holes in a consistent way. In fact there are black hole solutions which satisfy the string equations of motion. These equations of motion resemble the equations of general relativity with some extra matter fields coming from string theory. Superstring theories also have some special black hole solutions which are themselves supersymmetric, in that they preserve some supersymmetry.

One of the most dramatic recent results in string theory is the derivation of the Bekenstein-Hawking entropy formula for black holes obtained by counting the microscopic string states which form a black hole. Bekenstein noted that black holes obey an "area law", dM = K dA, where 'A' is the area of the event horizon and 'K' is a constant of proportionality. Since the total mass of black hole, 'M' is just the rest energy of the black hole, Bekenstein realized that this is similar to the thermodynamic law for entropy, dE = T dS. Hawking later performed a semiclassical calculation to show that the temperature of a black hole is given by T = 4 k [where k is a constant called the "surface gravity"]. Therefore the entropy of a black hole should be written as S = A/4. Following recent pioneering work by Strominger and Vafa, it has been found that this entropy formula can be derived microscopically (including the factor of 1/4) by counting the degeneracy of quantum states of configurations of strings and D-branes which correspond to certain supersymmetric black holes in string theory. That is to say, D-branes provide a short distance weak coupling description of certain black holes! For example, the class of black holes studied by Strominger and Vafa are described by 5-branes, 1-branes and open strings traveling down the 1-brane all wrapped on a 5-dimensional torus, which gives an effective one dimensional object -- a black hole.

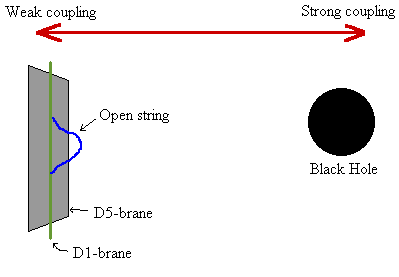
D-branes as black holes
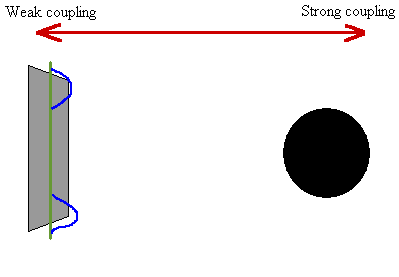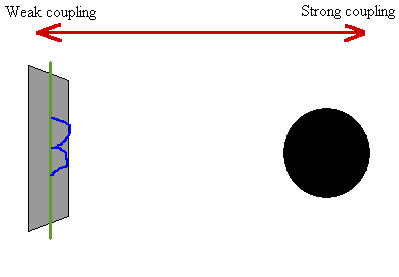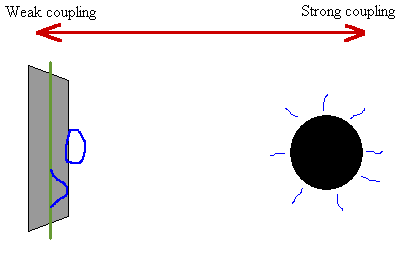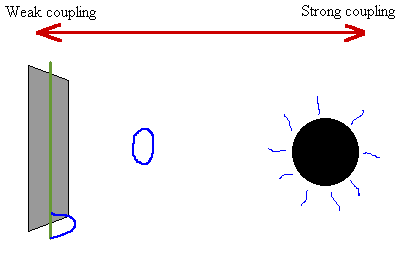
Hawking radiation can also be understood in terms of the same configuration, but with open strings traveling in both directions. The open strings interact, and radiation is emitted in the form of closed strings. The system decays into the configuration shown above.

Hawking radiation from D-branes

Explicit calculations show that for certain types of supersymmetric black holes, the string theory answer agrees with the semi-classical supergravity answer including non-trivial frequency dependent corrections called greybody factors.