Complex Systems

A granular material is a collection of distinct macroscopic particles, such as sand in an hourglass or peanuts in a container.  The evolution of the particles follows Newton's equations, with repulsive forces between particles that are non-zero only when there is a contact between particles.  Although granular materials are very simple to describe they exhibit a tremendous amount of complex behavior, much of which has not yet been satisfactorily explained.  They behave differently than solids, liquids, and gases which has led many to characterize granular materials as a new form of matter.

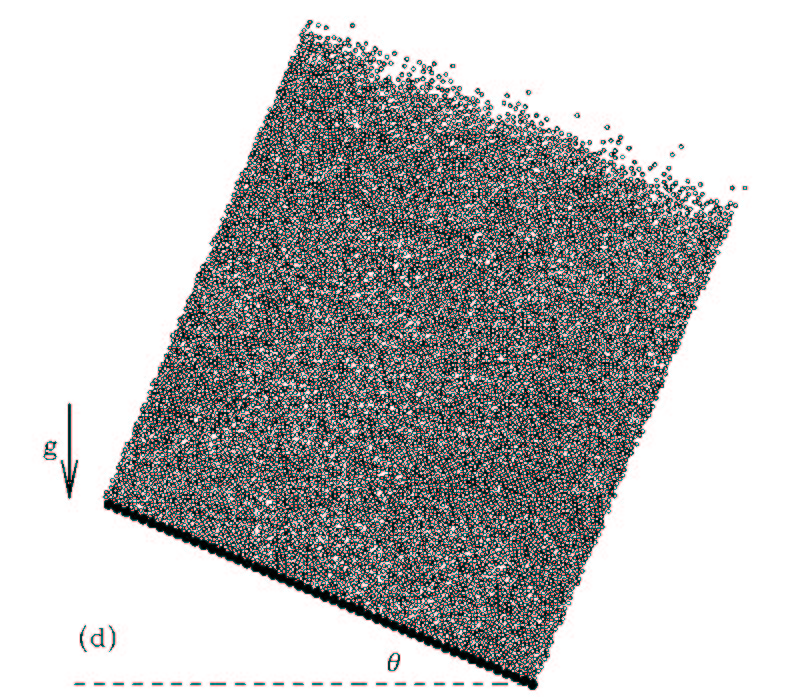A granular material on an incline plane, from simulations by Silbert and coworkers (2002)

For example, if a granular material is heaped on an inclined plane, then the large scale state of the system depends on the angle of the plane.  For large angles the granular material flows like a non-Newtonian liquid.  For small angles the granular material will behave like a solid and remain stationary.  The value of the critical angle between these phases depends on the preparation history, and the transition between the phases is a manifestation of the glass transition.  As you can see, there is a lot of interesting and complex physics to be understood by studying just the large scale properties of a granular material in such a simple arrangement.  As the composition becomes more complicated, the behavior becomes even richer.

From a small scale point of view, the characteristics that make granular materials interesting are inelastic collisions and the unimportance of temperature.  Because collisions between particles are inelastic then the energy of a granular material is a dynamic quantity, and because the particles that make up a granular materials are macroscopic then temperature does not produce significant motion.  Ultimately we would like to describe the properties of a granular material using statistical arguments, but since there is no well defined energy or temperature then conventional equilibrium statistical mechanics does not apply.  A full understanding of granular materials will require an extension of statistical mechanics, which is of great fundamental interest.  One central question concerning such a statistical theory is whether the robust yet fragile concept central to complexity in the  HOT  approach is apparent in a  granular material, which is very simple compared to ecological and biological systems.

A constitutive relation is an equation that relates the stress in a material to other known variables.  The common constitutive relation in fluid dynamics sets the stress proportional to the strain rate.  In granular materials this constitutive relation does not hold and evidence points to a quadratic relation between stress and strain rate.  In our work on granular materials, we concentrate on the 2-dimensional shearing geometry shown in figure 1.  The shearing geometry is interesting because what we learn can be applied to studies on friction and earthquakes.

In this geometry a shear stress s is applied to the top and bottom of the material and a confining pressure p keeps the material from expanding.  If s is large enough, the granular material will begin to move and eventually reach a steady state.  This steady state is characterized by an average velocity <v(y)>, which depends on the vertical position y, and an average squared velocity <v²> which does not depend on position.  The strain rate is defined as g = d<v(y)>/dt.  These average velocities must be somehow related to the stresses s and p.

In order to derive a constitutive equation we rely on the Shear Transformation Zone (STZ) theory of amorphous solids that was first proposed at UCSB by Falk and Langer.  STZ theory introduces variables that describe the internal, history dependent structure or state of a solid.  These variables describe the state of the solid by specifying the number of regions in a dense material that are able to move non-affinely in order to flow.   The shear rate can then be written in terms of the state variables.  STZ theory is an example of a rate and state law.  Combining STZ theory with a fundamental invariance in Newton's equations yields a relation between s, p, <v(y)>, and <v²>.

To test this relation we conduct computer simulations of sheared granular materials.  Figure 2 is a movie of one such simulation. With these simulations we can measure s, p, <v(y)>, and <v²> independently.  After many such simulations we obtain the data points shown in Figure 3.  The bottom curve is for a granular material with no friction between particles and the upper curve has some amount of friction between particles.  The line drawn through the data points is the prediction from STZ theory.  As you can see, the agreement is very good, and we were the first group to accurately predict this flowing constitutive relations for dense granular materials.

           Figure 2 :  A sample simulation                   Figure 3:  Data from simulations and fit from STZ
                                                                                      theory for s/p vs g/sqrt(<v²>)
 
 

We have learned a great deal applying STZ theory to granular materials, but there are still many open questions:

1. The constitutive relation in figure 3 only applies to steady state flow.  In the transient regime, where all of the variables have non-zero time derivatives, STZ theory makes predictions on their time dependence.  These predictions must be understood and tested.
2. STZ theory not only gives information about the flowing state of a granular material, but also makes predictions about how a granular material jams (transforms from liquid-like to solid-like behavior).  It is very important to understand and test these predictions as well.
3. Many properties of granular materials depend on the distribution of grain radii.  Figure 3 was obtained with one distribution and it would be interesting to know how the parameters in the STZ theory depend on the distribution of grain radii.
4. More conceptually, STZ theory is based on the fact that there are regions in a granular material that are able to transform non-affinely.  One interesting line of research is whether these regions are related to the force statistics and/or contact statistics of the granular material.
5. The study of sheared granular materials is closely related to the study of friction in earthquake faults .  This relation should be explored further.

We hope to undertake these projects soon.

Papers on STZ theory and its application to Granular Materials:
STZ Theory
Recent Papers

Questions?  Email Gregg Lois.

In order to calculate most any large scale parameter of a granular material (such as a stress), it is necessary to know the set of contacting particles and forces.   Because the large scale parameters are calculated from the small scale properties of individual grains, a general theory of granular materials must be able to predict these small scale properties.  While it is unlikely that any useful theory would be able to derive the exact small scale properties, a statistical determination would be very useful.

We have been working on creating simple theories that predict statistical measures.  The most interesting are: P(F), the probability density functional (PDF) to have a contact force of magnitude F;  <F(t)>, the PDF to have a contact force of magnitude F for a contact oriented with an angle(s) t;  and C(t), the PDF to have a contact oriented with angle(s) t.

The measure most studied in the physics literature is P(F).  For both flowing and jammed granular materials, P(F) is exponential at large forces.  At small forces the form of P(F) depends on the state of the granular material (see figure 1).  Most theoretical work has been concentrated on predicting P(F) for static, jammed granular assemblies.  Many of these theories use concepts from network theory or information theory.  We have been most interested in predicting P(F) for flowing configurations, and the work is ongoing.

Figure 1: Left:  Experimental P(F) for a jammed granular material from the granular physics group at Chicago.  This plot exhibits a peak at the average force. Right: P(F) for a flowing granular material from our simulations at UCSB.  The peak disappears.

The other two statistical measures are shown for a flowing granular material in figure 2.  The functional form is very similar for jammed granular materials.  The portion of these functions we have concentrated on predicting are the second fourier components.  This is because knowledge of the second fourier components of these measures is enough to determine the ratio of shear stress to pressure s/p (see constitutive relations for definitions of s and p) .   This work is also ongoing.

Figure 2: Left:  Number of contacts as a function of angle.  Right:  Average contact force as a function of angle
 

The interplay of the contact geometry and force distributions produces force chains which are  the paths of force propagation in a granular material.  We show pictures of force chains for jammed and flowing granular materials in figure 3.  These chains are heterogeneously distributed through the material and one line of research we are interested in is whether we can create a theory that predicts the locations of force chains and whether the regions with a high density of force chains are related to the regions that contain a high density of STZ's.  In a jammed material these chains tend to percolate throughout the entire enclosure and for flowing materials they tend not to.   This observation has led many to link the size of force chains with the onset of jamming.  This is another line of research that we are interested in.

Figure 3: Left - Force chains for a jammed granular material from an experiment by the Behringer group at Duke.  The size of the line represents the magnitude of contact force between grains.
Right-  Force chains for a flowing granular material from our simulations at UCSB.  A line is drawn between grains if there is a force (larger than some minimum value).
 

Questions?  Email Gregg Lois.