Complex Systems

Highly Optimized Tolerance (HOT) is a mechanism for power laws which blends the perspective of statistical physics with engineering methods for developing robust, highly interconnected systems. HOT states can arise through deliberate design or through natural selection, and are associated with high performance configurations in the midst of environmental uncertainty. This leads to non-generic, modular configurations which are "robust" to common perturbations, but especially "fragile" to rare events, unanticipated changes in the environment, and flaws in the design. Recently, HOT has been studied in the context of forest ecosystems, internet traffic, and power systems. In each case, HOT provides accurate fits to the statistical distribution of events. More importantly, HOT is leading to new, domain specific models for these systems which should lead to progress in understanding the special "fragile" sensitivities that accompany the high performance aspects of these systems.

Early work on HOT focused on simple models, contrasting their properties with existing literature aimed at providing a unifying framework for complex systems. This body of work includes Self Organized Criticality (SOC) as well as the Edge of Chaos (EOC), and emphasizes ideas from critical phase transitions, fractals, and bifurcations in dynamical systems. HOT also aims to provide a unifying framework, but emphasizes coupling to the external environment and the central role of robustness. In the highly designed HOT limit, the resulting complexity differs from SOC/EOC in almost every aspect. One of the most important differences has to do with sensitivities of systems to unanticipated changes in the environment or changes which have not been part of the evolutionary history of a system. HOT systems are "Robust yet Fragile"-robust to designed for perturbations, yet fragile, or hypersensitive, to rare events, design flaws, and new, unanticipated perturbations. Another important difference, is that while SOC/EOC explores generic states associated with bifurcations and phase transitions, HOT states are exceedingly rare and specialized to the environment and history. This strong connection between the evolution of the system and the environment to which it is coupled makes HOT systems specially vulnerable to environmental change. To date, HOT has been strikingly successful in capturing features of real world complex systems, and is leading to new insights as the work is extended towards specific applications.

Percolation forest fire models are a familiar template for studying complexity and a starting point for HOT. Percolation is the simplest model which exhibits a critical phase transition. Sites on a two-dimensional square lattice are occupied (trees) or vacant (firebreaks). Contiguous sets of nearest neighbor occupied sites define connected clusters. The forest fire model includes a coupling to external disturbance, modeled by sparks which impact individual sites, burning through the corresponding connected cluster. In the HOT version, the goal is to optimize yield, defined to be the density remaining after a single spark. I have investigated a variety of different optimization schemes, including optimal placement of vertical and horizontal strips of vacancies amidst an otherwise full lattice, growth of an optimal forest by placing trees in the best location one at a time, optimizing local densities in coarse grained regions of a superimposed design grid, and Darwinian evolution by mutation and natural selection. All of these lead to similar results. Optimized lattices consist of compact cellular regions of contiguous tress, separated by efficient linear barriers formed by vacancies. These robustness barriers are concentrated in regions where sparks are common, and sparse in regions where sparks are rare. Barriers to cascading failure is a useful abstraction for robustness mechanisms in real systems. In some cases, barriers are physical constraints (such as skin, cell walls, and highway lane dividers). However, barriers may also occur in a system's state space, constructed via complex, regulatory feedback loops in the system's dynamics (such as immune systems, and the TCP/IP protocol suite). The lattice models illustrate the emergence of robustness barriers and other key features associated with HOT, including (1) high efficiency, performance, and robustness to designed-for uncertainties, (2) hypersensitivity to design flaws and unanticipated perturbations, (3) nongeneric, specialized, structured configurations, and (4) power laws.

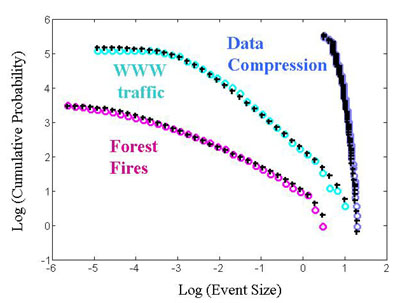An early, quantitative success of HOT was obtained by generalizing Shannon Coding from Information Theory. This is the PLR model, defined by probabilities P, describing the relative likelihood of a set of events, losses L, describing the associated cost, and resources R, which constrain the loss. The PLR problem involves optimization of the allocation of limited resources to minimize the expected loss over the spectrum of possible events. In the case of forest fires, the resources might be firebreaks or other means of suppression. In the case of World Wide Web traffic, the analog of sparks are hits by users browsing a site, and optimization arises in dividing documents into a limited number of files in a manner which minimizes congestion of the server. The success of PLR theory lies in the striking accuracy with which it describes statistical distributions for the size and frequency of forest fires, World Wide Web downloads, and electric power outages.