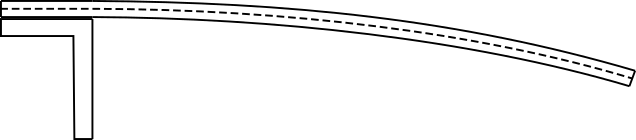
Two wood beams of equal length and width, one about 1.76 times the height of the other, are supported near one end. The other end is free. You can observe the difference in deflection between the free ends of the two boards with no added load, and you can set a mass of the end of each board and note the difference in the change in deflection of each board for a given load.
Shown above are two boards that are 200 cm (79″) long, which when set on the black support at left, have a free length of 170 cm (67″). (For the purposes of this demonstration, we assume that the part of each board between the edge of the support and the lead brick remains flat.) Both boards are 3.9 cm (1.5″) wide. One board is 8.3 mm (0.33″) thick, and the other is 14.6 mm (~0.575″) thick. (Measurements with a caliper give 14.6 mm (0.575″) and 8.28 mm (0.327″). The masses of the free lengths of the boards are 330 g and 580 g, respectively. (The total masses of the two boards are 390 g and 680 g, respectively.) 100-g and 200-g masses are available to set on the ends of the boards, or at various other points, to show how the deflection varies according to where you place the load, and how it depends on the size of the load. You can compare the deflections of the unloaded boards, and of the boards with different loads set on them. A small plastic ruler allows you to measure the width and thickness of each board, and a 2-meter stick allows you to measure the free length of the boards, and to estimate the deflection. The top surfaces of the fixed ends of the boards sit about 109.0 cm (thicker board) and 108.5 cm (thinner board) above the floor when the boards are as shown above. With the boards unloaded, the top surfaces at the free ends sit about 105.9 cm and 94.3 cm, respectively, above the floor. These correspond to deflections of about 3.1 cm and 14.2 cm, respectively.
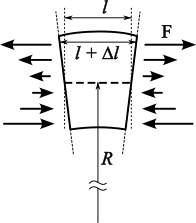
This demonstration is an illustration of shear forces, that is, forces that are applied parallel to the plane of cross section of a material. When so applied, these are known as shear stresses. Such forces are illustrated in demonstrations 32.24 -- Shearing of foam logs, and 32.27 -- Book shear, and bear comparison to normal stresses, such as that illustrated in demonstration 32.21 -- Stretch wire to breaking point, which is perpendicular to the cross section of the material (and in this case is a tensile stress). The boards shown above are supported horizontally at one end and free at the other end, to form cantilevers. Gravity, in acting along the length of each board, acts parallel to its vertical cross section, and thus constitutes a shear force along the length of the board and causes them to bend downward from the fixed end. The material at the top of each board is being stretched – it is under tension, and the material at the bottom of each board is being compressed – it is under compression. These tensile and compressive forces act along planes parallel to the top and bottom surfaces of the boards; they are shear forces. In the (horizontal) plane along the middle of the boards, the material is neither stretched nor compressed; this plane is called the neutral surface. This surface is represented by the dotted line in the diagram below, which illustrates one of the bent boards.
The tensile force in the material above the neutral surface and the compressive force in the material below the neutral surface are proportional to the distance above or below the neutral surface, as is the resulting deformation. The diagram below will be useful in the analysis that follows:
After Fig. 38-12 in Feynman, Richard P., Leighton, Robert B., and Sands, Matthew. The Feynman Lectures on Physics, Volume II (Menlo Park, California: Addison-Wesley Publishing Company, 1967), p. 38-9.
The diagram above represents a side view of a small section of the board shown in the first diagram. The dashed line is the neutral surface, and the arrows represent the tensile forces above the neutral surface and the compressive forces below it. l is the length of the undeformed section (which remains the same at the neutral surface), and l + Δl is the length of the deformed section at a point some distance y above or below the neutral surface. R is the radius of curvature of the bent section, which determines the relationship between the the amount of stretch or compression and the distance from the neutral surface, Δy:
Δl/l = y/R
If we imagine a small strip across the beam, of a thickness Δy (a thin horizontal portion of the cross section of the beam), the force per unit area is also proportional to the distance from the neutral surface:
ΔF/ΔA = Y(y/R)
Here, Y is the Young’s modulus of the material, the ratio of the force applied per unit area to the deformation, or the stress divided by the strain. (In engineering contexts it is usually denoted E, and called the modulus of elasticity or elastic modulus.) Since the material in the beam is stretched above the neutral surface and compressed below it, if we examine either side of the diagram above, we see that the forces above and below the neutral surface are in opposite directions. They thus form pairs that exert a torque about a line on the neutral surface, which we may call a bending moment. The total moment is the integral of the force times the distance from the neutral line over the cross-sectional area of the beam, or
𝔐 = ∫ y dF
Since dF = (Y/R) y dA, we have
𝔐 = (Y/R) ∫ y2 dA
Probably because this bending is a type of rotation, and because of the similarity of this integral to that for the moment of the mass in a rotating object, the integral ∫ y2 dA is known as the moment of inertia, and is denoted I, and the bending moment is
𝔐 = YI/R
The bending moment is a measure of the stiffness of the beam, and is determined by the Young’s modulus and the moment of inertia together. From the diagram above, and from the integral for the moment of inertia, we see that the farther material is from the neutral surface, the more greatly it contributes to the moment of inertia, and thus to the stiffness of the beam. Given constraints on weight, or limited material, it is advantageous to use a type of cross-section that puts a significant portion of the mass of the beam far from the neutral surface. This is why the I beam (whose cross-section resembles the shape of an I with more or less wide serifs) is such a common shape in construction. All of this would indicate that the moment of inertia for a particular beam varies according to both the shape and dimensions of its cross section. For a rectangular beam such as the two in this demonstration, the integral above is straightforward. If we call the width of the beam w and the thickness of the beam h, it is:
w-h/2∫h/2 y2 dy = (w/3)[(h/2)3 - (-h/2)3] = (w/3)(h3/4) = wh3/12
We see that the stiffness goes as the cube of the thickness, and linearly in the width. Since the two boards above have the same width, but differ in thickness by a factor of about 1.76, to produce a given deflection, the load on the thicker board should be about 1.763 times, or about 5.5 times, that on the thinner board.
Now we’ll examine the relationship between the length of a cantilever and the deflection of its free end under a given load placed there. We’ll call the length of the cantilever L, distance from the fixed end x, and the deflection at any given distance z. We consider small deflections, and assume that the length of the cantilever is much greater than its thickness. The curvature of z(x) is:
(1/R) = (d2z/dx2)/[1 + (dz/dx)2]3/2
For small slopes, (dz/dx)2 is small compared to 1, and we may neglect it. This gives:
(1/R) = (d2z/dx2)
Because the bending moment, 𝔐, is the torque about the neutral axis of any cross section, it is a function of x. Not including the weight of the beam, for a given load, W, at the end of the beam, the bending moment at a distance x is:
𝔐(x) = W(L - x)
Recalling that 𝔐 = YI/R, we have:
W(L - x) = YI/R = YI (d2z/dx2)
which we can rearrange to:
(d2z/dx2) = (W/YI)(L - x)
If we set z(0) to zero, and dz/dx = 0 at x = 0, this integrates to:
z = (W/YI)[(Lx2/2) - (x3/6)]
At the end of the cantilever, x = L, and:
z(L) = (W/YI)(L3/3)
We see that the displacement at the end of the cantilever increases as the cube of its length. You can show this by sliding the beams to leave shorter sections hanging free and comparing the deflections you observe for different free lengths.
References:
1) Feynman, Richard P., Leighton, Robert B., and Sands, Matthew. The Feynman Lectures on Physics, Volume II (Menlo Park, California: Addison-Wesley Publishing Company, 1967), pp. 38-9, 38-10.
2) There are probably many places where you can find information about structural members. One very interesting source is Machinery’s Handbook, which is a comprehensive collection of information about materials, machining and tooling, and mathematics used in working with these things. On pages 358 to 367, the 1959 edition of this book has tables that give moments of inertia and other related characteristics of beams of various cross sections. The reference is: Oberg, Erik and Jones, F. D.; Horton, Holbrook L., Ed. Machinery’s Handbook – A Reference Book for The Mechanical Engineer, Draftsman, Toolmaker, and Machinist, Sixteenth Edition, Second Printing (New York: The Industrial Press, 1959), pp. 358-359. More recent editions are available.