Current Work
- Research Overview
- Localization in amorphous solids
- Fluid/compliant membrane
- Avoiding spurious eigenvalues
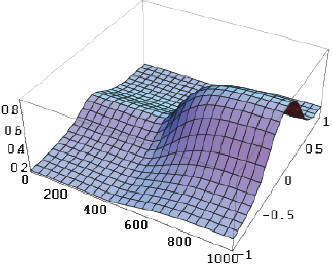
Effective disorder temperature as a function of position and time shows localization.
Earlier Work
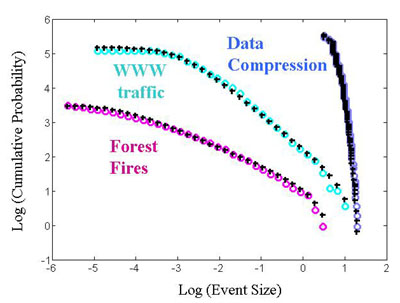
The probability-loss-resource HOT model predicts the cumulative probability for events of a given size.
Research overview
I am interested in developing and analyzing continuum models for dynamical systems that initially do not seem amenable to continuum descriptions. These systems, including fluids and amorphous solids, are ubiquitous and familiar, and are studied in a variety of fields, including soft condensed matter physics, materials, and mechanical engineering.
Continuum descriptions such as the Navier-Stokes equations or linear elasticity are sometimes useful for predicting macroscopic behavior. However, many of these dynamical systems contain many degrees of freedom, and can undergo a transition from relatively simple macroscopic motion described by a few parameters to a much more complicated motion where smaller length scales become important and the original continuum description fails. In fluids, a laminar flow transitions to a turbulent one, and in amorphous materials a sheared material develops a highly localized shear band. We want to understand what mechanisms underlie these transitions.
My work shows that with a little work, the continuum description is still a valuable predictive tool for these systems. In fluids, a broader definition of stability helps us understand transition to turbulence using only the linearized Navier Stokes equations. In amorphous materials, the effective temperature is an additional parameter that specifies the state of the system. Analyzing the steady state and transient dynamics of this variable suggests a mechanism for strain localization.
Localization in an STZ model for amorphous materials
Amorphous materials often comprise or lubricate sheared material interfaces and require more complicated constitutive equations than simple fluids or crystalline solids. They flow like a fluid under large stresses, creep or remain stationary under smaller stresses, and have complex, history-dependent behavior. Bulk metallic glasses, granular materials, and bubble rafts are just some of the disordered materials that exhibit a yield stress.
Strain localization is the spontaneous development of coexisting flowing and stationary regions in a sheared material. Strain localization has been identified and studied experimentally in granular materials, bubble rafts, complex fluids, and bulk metallic glasses. Shear banding may play an important role in the failure modes of structural materials and earthquake faults. Localization is a precursor to fracture in bulk metallic glasses and has been cited as a mechanism for material weakening in granular fault gouge on faults.
We model amorphous solids with a set of partial differential equations that describe Shear Transformation Zones (STZs) (Falk and Langer, 1998) with an effective temperature. We find small perturbations in the effective temperature can lead to localized regions of higher strain, or shear bands, in our numerically integrated solution, and show that the system is linearly unstable with repect to perturbations to a time-varying trajectory.
We are also interested in using STZs equations that exhibit localized shear regions to generate a constitutive relations for interfaces between sheared materials (such as fault planes in earthquakes). Shear banding should be a strong velocity-weakening mechanism which has important implications for friction laws in these systems.
Localization in an STZ model for amorphous materials
Transition to turbulence in fluid flowing past a compliant boundary
In the fluid/compliant wall system, we are interested in determining how the coupling of elastic equations for the wall with the Navier-Stokes equations for the fluid might hasten or delay transition to turbulence in channel flows. We perform an input/output analysis of the system. This is a generalized stability analysis that captures highly amplified modes in addition to those which are linearly unstable.
Notes on fluid/compliant wall problem
Spurious Eigenvalue problem
Spurious eigenvalues are unphysical, numerically-computed eigenvalues with large positive real parts that often occur in hydrodynamic stability problems. We propose that these unphysical eigenvalues are possible in the analysis of any set of differential-algebraic equations when the number of independent variables is analytically reduced using the algebraic constraints and the system is subsequently approximated using finite difference or spectral collocation methods.
An alternative approach to analyzing differential-algebraic equations is the descriptor framework, posed as a generalized eigenvalue problem, which explicitly retains the algebraic constraints during the numerical computation of eigenvalues. We reformulate two common hydrodynamic stability problems using descriptor notation and show that this method of computation avoids the spurious eigenvalues generated by other methods. The descriptor formulation is a simple, robust framework for eliminating spurious eigenvalues that occur in hydrodynamic stability analysis and in the study of other dynamical systems with algebraic constraints. Additionally, this formulation reduces the order of the numerically approximated differential operators and accommodates complex boundary conditions, such as a fluid interacting with a flexible wall.
Earlier Studies and Outside Interests
Highly Optimized Tolerance
Optimization-based models for complex systems that exhibit robust yet fragile behavior
I have also studied systems that generate distributions with heavy tails or power law behavior. In the past, these power laws have been explained by several different mechanisms including preferrential growth, self organized criticality (SOC), highly optimized tolerance (HOT), and allometry (scaling with biological mass). I am interested in how the different mechanisms generate power laws with different exponents and cutoffs. For example, different HOT models predict different exponents for distributions from similar systems. We determined that these different HOT models describe two separate regimes -- one where there are a lot of resources that can be used to prevent large, cascading events, and one where there are few resources available.
Highly Optimized Tolerance in dense and sparse resource regimes
Mixtures
I have also studied mixture models. We would like to determine what happens when several data sets which have a power-law distribution (with large and small-scale cutoffs) are mixed together indescriminately.